Rydberg equation – Examples, Definition, Formula, Uses, FAQ’S

The Rydberg Formula is a critical tool in physics that calculates the wavelengths of spectral lines for various chemical elements. It specifically predicts the wavelengths of photons emitted as electrons transition between energy levels within an atom, particularly in hydrogen. This formula is instrumental in exploring atomic structures and the fundamentals of quantum mechanics, aligning closely with the laws of physics and providing insights that bridge classical and quantum theories.

What Is Rydberg Formula?

Rydberg Formula

The Rydberg Formula is used to calculate the wavelengths of the spectral lines of hydrogen and hydrogen-like elements. It is expressed as:

where:

• λ is the wavelength of the emitted or absorbed light,
• 𝑅 is the Rydberg constant (approximately 1.097×10⁷ m⁻¹),
• 𝑛₁ and 𝑛​₂ are the principal quantum numbers of the lower and upper energy levels of the electron transition, respectively, with 𝑛₂>𝑛₁​.

This formula is crucial in spectroscopy for identifying elements and understanding atomic structure.

Rydberg Formula Derivation

The derivation of the Rydberg Formula for the hydrogen atom involves understanding how energy levels in an atom relate to the frequencies (and thus wavelengths) of light emitted or absorbed when an electron transitions between these levels. Here’s a step-by-step explanation:

Step 1: Energy Levels of the Hydrogen Atom

The energy of an electron in a hydrogen atom can be expressed by the Bohr model as:

Where:

• 𝐸𝑛​ is the energy of the nth energy level,
• 𝑍 is the atomic number (for hydrogen, 𝑍=1),
• 𝑅𝐻​ is the Rydberg constant for hydrogen,
• 𝑛 is the principal quantum number.

Step 2: Photon Emission and Absorption

When an electron transitions from a higher energy level 𝑛₂ to a lower energy level 𝑛₁​, it emits a photon whose energy 𝐸E corresponds to the difference between these two energy levels:

Step 3: Relation to Photon Wavelength

The energy of the photon can also be related to its wavelength 𝜆 through the Planck relation:

Where:

• ℎ is Planck’s constant,
• 𝜈 is the frequency of the photon,
• 𝑐 is the speed of light.

Step 4: Combine Equations

Equating the two expressions for energy, we get:

ℎ⋅𝑐/𝜆=𝑅𝐻/𝑛²₁−𝑅𝐻/𝑛²₂λ​​

Rearranging for 𝜆λ, we find the Rydberg Formula for the wavelengths of emitted photons:

1/𝜆=𝑅(1/𝑛²₁−1/𝑛²₂)

Where R is the Rydberg constant for hydrogen, often used in the more general form adjusted for the specific atom by taking into account 𝑍 and Rₕ​.

Rydberg Formulas for Different Units

Here’s a table presenting the Rydberg Formula for hydrogen, the general formula for wavelength, and the values of the Rydberg constant in different units:

This table encapsulates the critical aspects of the Rydberg Formula and the constant, providing essential details for calculations involving atomic spectra, particularly for hydrogen.

Uses of Rydberg Formula

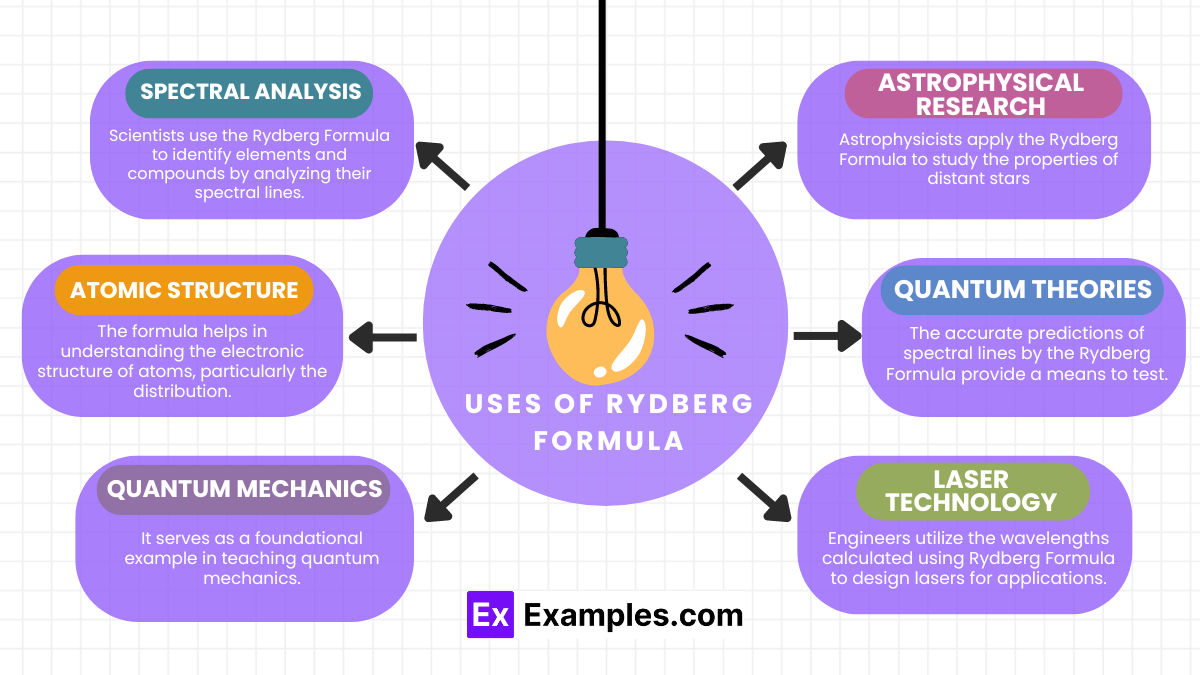
The Rydberg Formula has several important applications in physics and chemistry:

• Spectral Analysis: Scientists use the Rydberg Formula to identify elements and compounds by analyzing their spectral lines. This is crucial in both laboratory research and astronomical spectroscopy.
• Determining Atomic Structure: The formula helps in understanding the electronic structure of atoms, particularly the distribution and energy levels of electrons.
• Quantum Mechanics Education: It serves as a foundational example in teaching quantum mechanics, illustrating the quantization of atomic energy levels.
• Astrophysical Research: Astrophysicists apply the Rydberg Formula to study the properties of distant stars and galaxies by observing the spectral lines emitted from these celestial bodies.
• Testing Quantum Theories: The accurate predictions of spectral lines by the Rydberg Formula provide a means to test and validate various quantum mechanical theories and models.
• Laser Technology Development: Engineers utilize the precise wavelengths calculated using the Rydberg Formula to design lasers for specific applications, including medical procedures and optical communications.

Examples for Rydberg Formula

Here are some examples illustrating the practical applications of the Rydberg Formula, enriched with transition words to clarify the flow of ideas:

1. Hydrogen Spectrum Analysis: Initially, the Rydberg Formula is used to calculate the wavelengths of the hydrogen emission spectrum. This includes the well-known Balmer series, visible to the naked eye, which arises when electrons transition from higher energy levels to the second energy level.
2. Astronomical Spectroscopy: Furthermore, astronomers apply the Rydberg Formula to identify elements present in stars and galaxies. By measuring the wavelengths of light from celestial objects and matching them to known spectral lines predicted by the Rydberg Formula, they can determine the composition of distant stars and galaxies.
3. Quantum Mechanics Demonstrations: Additionally, educators use the Rydberg Formula in academic settings to demonstrate the quantum mechanical model of the atom. It provides a clear example of how electron transitions between energy levels lead to the emission or absorption of light at specific wavelengths.
4. Laser Technology Development: Moreover, researchers utilize the Rydberg Formula in developing and refining laser technologies. By understanding the precise wavelengths involved in electron transitions, they can engineer lasers that operate at specific frequencies for applications in medicine, communications, and manufacturing.

These examples underscore the versatility and fundamental importance of the Rydberg Formula in both theoretical and applied physics.

FAQ’S

Is Rydberg equation only for hydrogen?

No, the Rydberg equation originally formulated for hydrogen can also be modified to apply to hydrogen-like (single-electron) ions of other elements.

Does the Rydberg equation work for all elements?

The Rydberg equation works primarily for elements with a single electron in their outer shell, such as hydrogen-like ions, but not for multi-electron atoms.

Why does the Rydberg equation work for hydrogen but not for helium?

The Rydberg equation works for hydrogen because it has one electron. For helium and other multi-electron atoms, electron-electron interactions complicate the spectrum, making the equation ineffective.