Triangle Law of Vector Addition

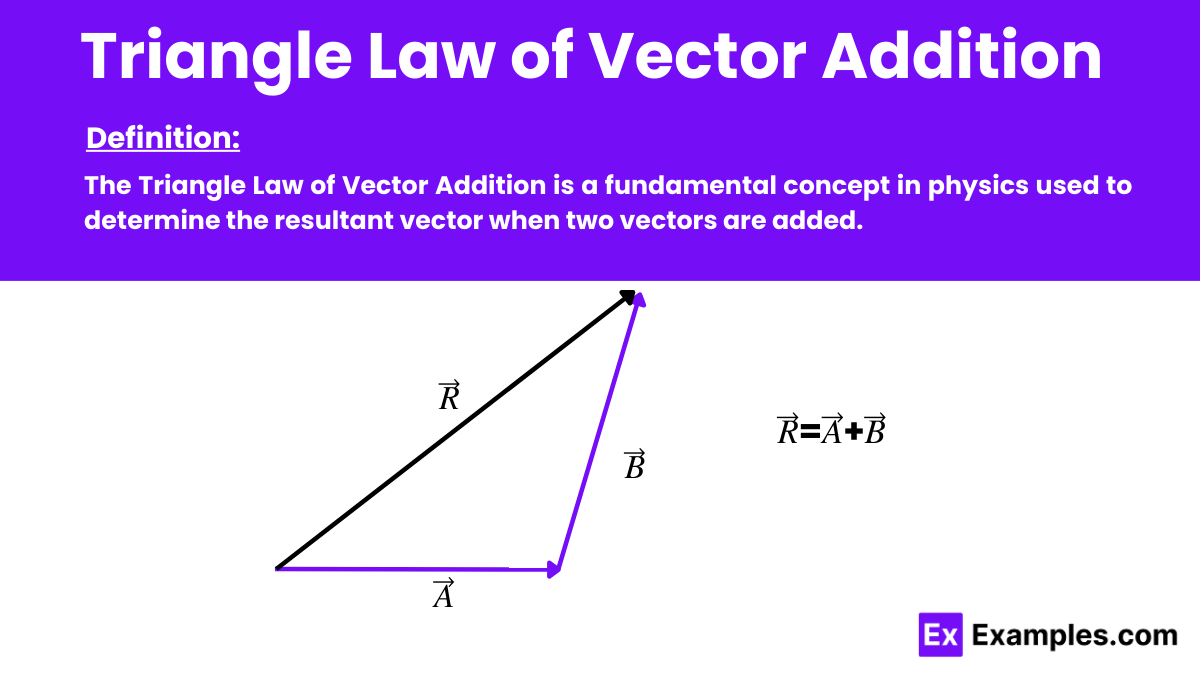
The Triangle Law of Vector Addition is a fundamental concept in physics used to determine the resultant vector when two vectors are added. This law states that if two vectors are represented by two sides of a triangle taken in order, then the resultant vector is represented by the third side of the triangle taken in the reverse order.

What is Vector Addition?

Vector addition is the process of combining two or more vectors to produce a resultant vector. This operation is essential in physics to understand how different vectors like forces, velocities, or accelerations interact with each other.

To perform vector addition, you can use either the graphical method or the algebraic method. The graphical method involves drawing vectors on a graph based on their magnitude and direction. Starting the next vector from the endpoint of the previous one. The final vector, drawn from the origin of the first vector to the endpoint of the last, represents the resultant vector.

What is Triangle Law of Vector Addition?

The Triangle Law of Vector Addition is a rule used to determine the resultant vector when two vectors are added together. This law is crucial in physics for combining different vectors, such as forces or velocities.

According to the Triangle Law of Vector Addition, if you represent two vectors as two sides of a triangle. It is taken in a specific order, then the resultant vector is represented by the third side of the triangle. It is taken in the opposite order. Essentially, this method involves placing the tail of the second vector at the head of the first vector. The line drawn from the tail of the first vector to the head of the second vector then represents the resultant vector.

Triangle Law of Vector Addition Formula

Formula

If:

• 𝐴⃗ and 𝐵⃗ are two vectors being added,
• The resultant vector 𝑅⃗ is given by:

𝑅⃗=𝐴⃗+𝐵⃗

Graphical Representation

1. Arrange 𝐴⃗: Place vector 𝐴⃗ starting at any point.
2. Position 𝐵⃗: Place the tail of vector 𝐵⃗ at the head of vector 𝐴⃗.
3. Draw Resultant 𝑅⃗: Draw the resultant vector 𝑅⃗ from the tail of 𝐴⃗ to the head of 𝐵⃗.

This arrangement forms a triangle if vectors 𝐴⃗, 𝐵⃗, and 𝑅⃗ are depicted graphically, thus demonstrating the Triangle Law of Vector Addition.

Triangle Law of Vector Addition Derivation

Let’s consider two vectors 𝐴⃗ and 𝐵⃗ and assume they form an angle 𝜃=45⁰ with each other.

Representation in a Triangle:

Place vector 𝐴⃗ with its tail at the origin.

Place vector 𝐵⃗ such that its tail begins at the head of 𝐴⃗.

Constructing the Triangle:

Draw the resultant vector 𝑅⃗ from the tail of 𝐴⃗ to the head of 𝐵⃗. This vector 𝑅⃗ represents the sum 𝐴⃗+𝐵⃗.

Calculating the Magnitude of 𝑅⃗:

• According to the law of cosines in a triangle:

∣𝑅⃗∣²=∣𝐴⃗∣²+∣𝐵⃗∣²+2∣𝐴⃗∣∣𝐵⃗∣cos⁡𝜃

• Substituting 𝜃=45⁰:

∣𝑅⃗∣²=∣𝐴⃗∣²+∣𝐵⃗∣²+2∣𝐴⃗∣∣𝐵⃗∣cos⁡45⁰

• With cos⁡45⁰=√2/2​​:

∣𝑅⃗∣²=∣𝐴⃗∣²+∣𝐵⃗∣²+√2∣𝐴⃗∣∣𝐵⃗∣

Taking the square root gives the magnitude of 𝑅⃗.

Direction of 𝑅⃗:

• To determine the direction, use the sine rule:

∣𝐴⃗∣/sin⁡∠𝐵=∣𝐵⃗∣/sin⁡∠𝐴=∣𝑅⃗/∣sin⁡∠𝐶

where ∠𝐴, ∠𝐵, and ∠𝐶 are the angles opposite to 𝐴⃗, 𝐵⃗, and 𝑅⃗, respectively.

Conclusion:

The triangle constructed with 𝐴⃗ and 𝐵⃗ demonstrates that their resultant, 𝑅⃗, represents their vector sum.

This derivation confirms the Triangle Law of Vector Addition, showing that the resultant vector’s magnitude and direction can be calculated using trigonometric principles.

Uses of Triangle Law of Vector Addition

The Triangle Law of Vector Addition is highly versatile and finds applications in various fields, particularly in physics. Here are some of the key uses:

• Force Analysis: Engineers and physicists use the Triangle Law to calculate the resultant force when multiple forces act on an object. This is crucial for understanding equilibrium, stability, and motion of structures or mechanical systems.
• Navigation: The law assists in navigation by helping to determine the actual path or displacement of a vehicle or ship. When it moves with successive vectors of speed and direction changes.
• Physics Education: It serves as a fundamental teaching tool in vector algebra, helping students visualize and understand vector addition, which is essential for more complex physics problems.
• Robotics: In robotics, the Triangle Law is used to compute resultant vectors for motion planning and control, allowing robots to navigate and perform tasks effectively in dynamic environments.
• Computer Graphics: This law is applied in computer graphics for animations and simulations where multiple vector forces need to be combined to create realistic movements and effects.
• Meteorology: Meteorologists apply this law to predict wind directions and speeds by combining different wind vectors to understand complex weather systems better.

FAQ’S

What are the three laws of vector addition?

The three laws of vector addition are the Triangle Law, Parallelogram Law, and Polygon Law.

Is it possible to add two velocities using triangle law?

Yes, it is possible to add two velocities using the Triangle Law by placing them head-to-tail and drawing the resultant vector.

Are triangle law and parallelogram law the same?

No, the Triangle Law and Parallelogram Law are not the same. However, they are related and can both be used to find the resultant vector.