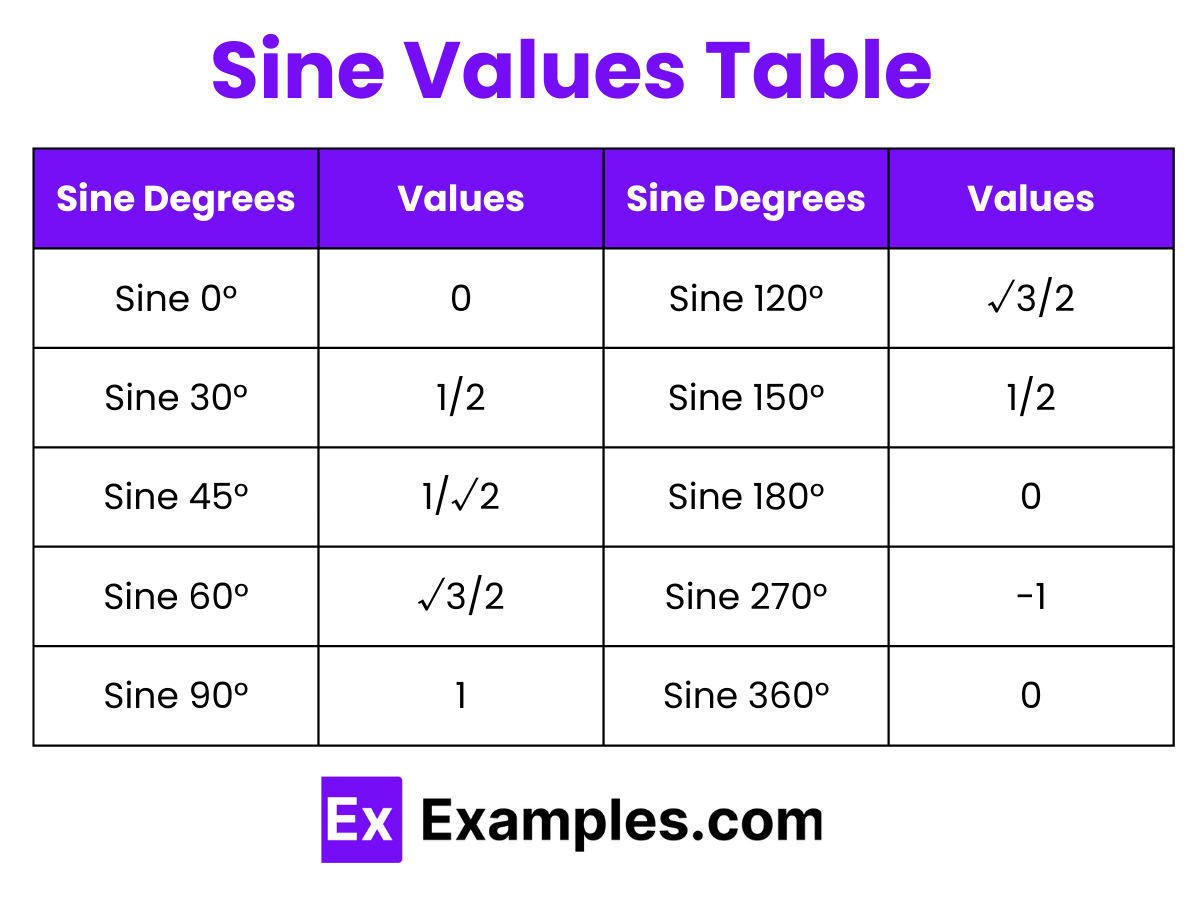
What is the sine of 30 degrees?
0.5
0.6
0.7
0.8

The sine function is a pivotal concept in trigonometry, a branch of mathematics that explores the relationships between angles and side lengths in triangles. It’s defined by the trigonometric formula sin(θ)=opposite/hypotenuse, making it essential for calculating angles and dimensions in various fields such as engineering, physics, and even art. Comprehensive resources, including detailed trigonometry formula PDFs, provide invaluable tools for students and professionals alike to deeply understand and apply these principles. These documents often encapsulate not only the sine function but also other trigonometric functions, enriching one’s math toolkit. As trigonometry continues to evolve, these foundational formulas remain at the heart of understanding complex geometrical and real-world phenomena.
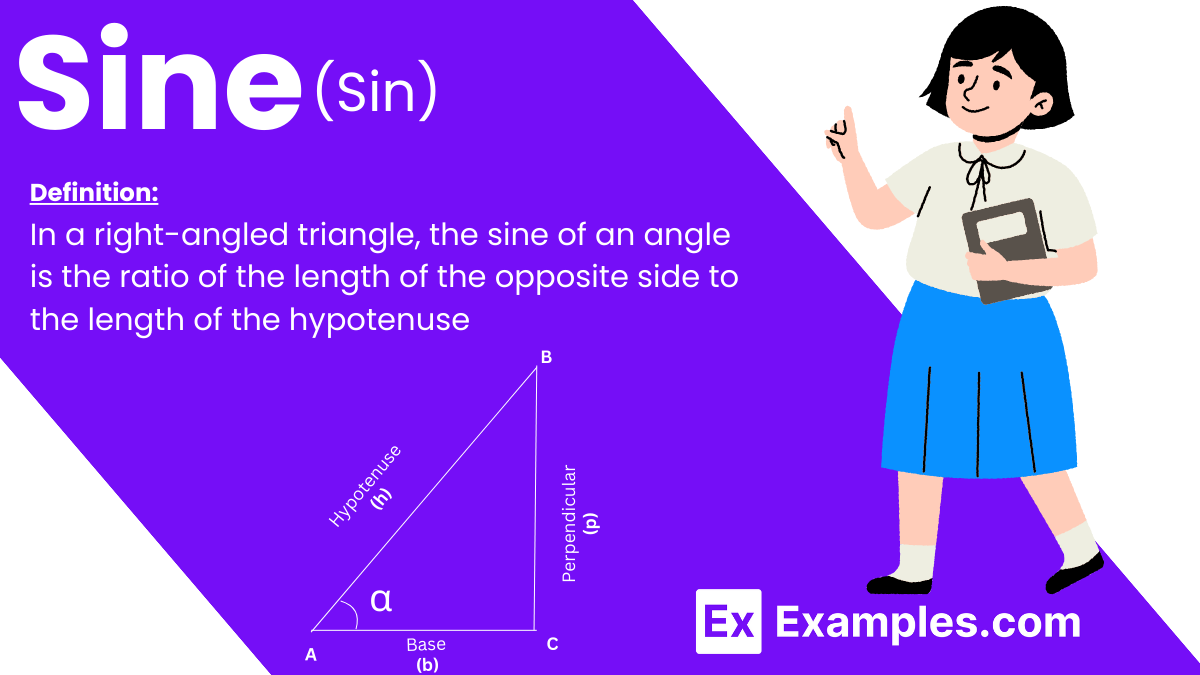
Sine is a fundamental concept in trigonometry, a branch of mathematics dealing with the relationships between the angles and sides of triangles. In a right-angled triangle, the sine of an angle is the ratio of the length of the opposite side to the length of the hypotenuse.

The sine function, often abbreviated as “sin,” is a crucial part of trigonometry. Here are the key formulas and representations involving sine:
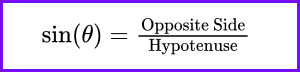
In a right-angled triangle, the sine of an angle θ\thetaθ is defined as the ratio of the length of the opposite side to the length of the hypotenuse. The formula is:
On the unit circle, where the radius is 1, the sine of an angle θ is the y-coordinate of the point on the circle corresponding to that angle. The formula is:
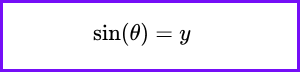
For a point (x,y) on the unit circle corresponding to an angle θ:
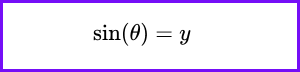
For a given angle θ:

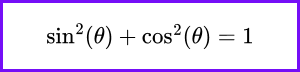
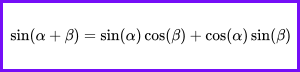

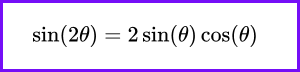
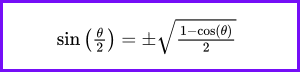
The graph of the sine function is a wave that oscillates between -1 and 1, with a period of 2π. It is defined for all real numbers θ
sin(θ) is periodic with period 2π, which means:
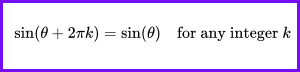
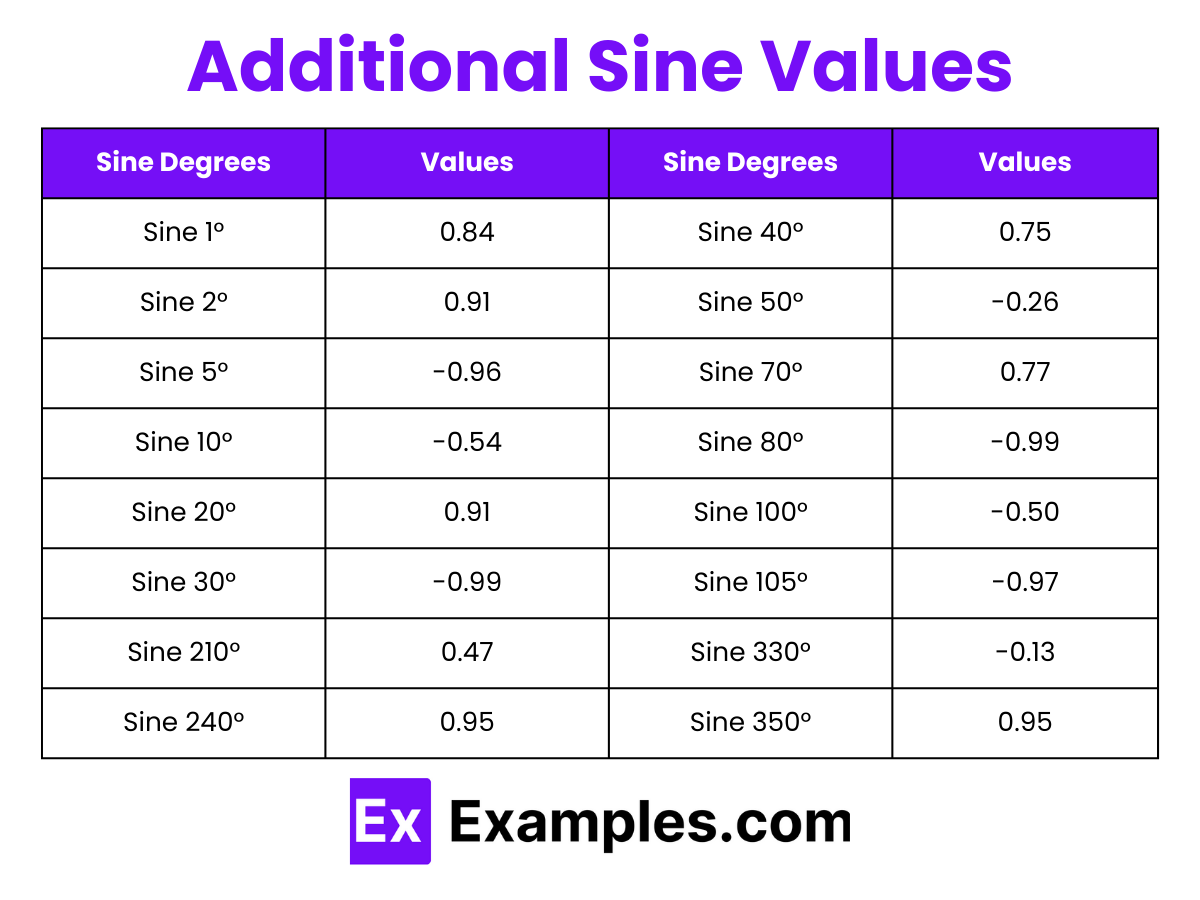
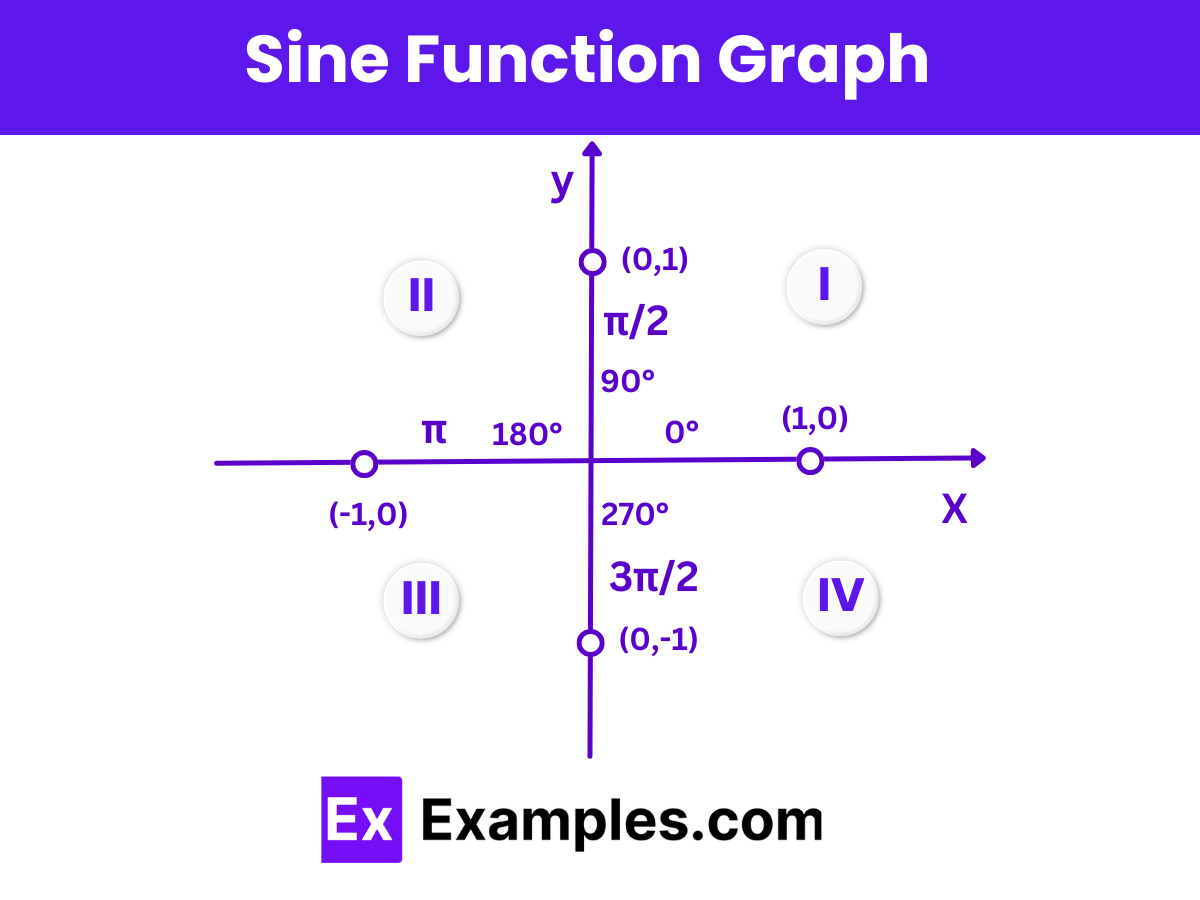
The sine function, sinθ, exhibits specific properties depending on the quadrant in which the angle θ lies. The behavior of the sine function across the four quadrants is an important aspect of trigonometry. Here’s a breakdown of these properties:
The sine function, y=sin(x), is defined for all real numbers, making its domain the entire set of real numbers, denoted as R. The range of the sine function is the closed interval [−1,1], indicating that the values of y, or sin(x), are confined between −1 and 1 inclusive (−1≤y≤1 or −1≤sin(x)≤1). Additionally, the behavior of the sine function’s range varies depending on the quadrant of the angle x. Below is a table that delineates how the range of the sine function adjusts according to different quadrants:
he sine function, sin(x), is integral to calculus, offering numerous applications ranging from basic differentiation and integration to solving complex differential equations and modeling periodic phenomena. Here’s how the sine function is utilized in various aspects of calculus:
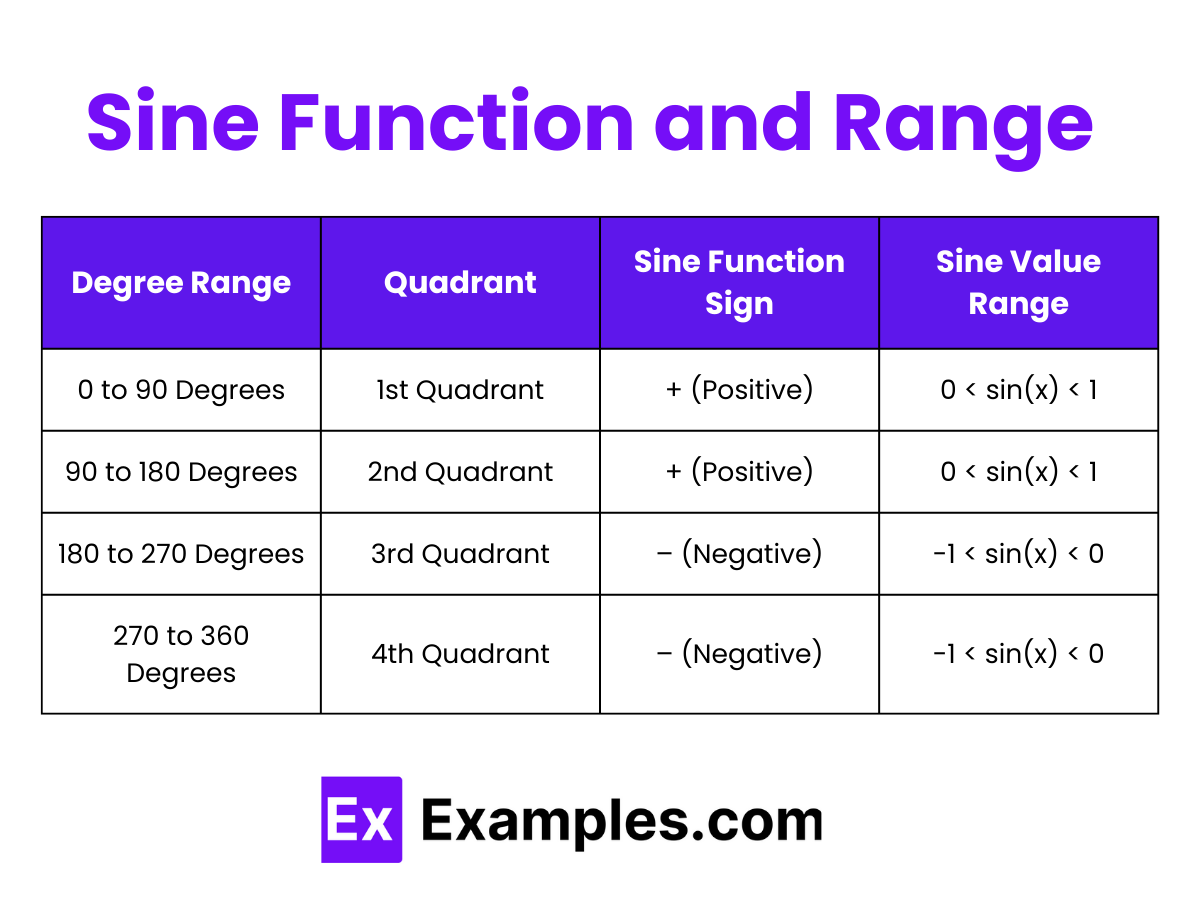
The derivative of the sine function is a foundational concept in calculus. The derivative of sin(x) with respect to x is cos(x):
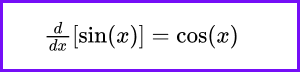
This property is particularly important when analyzing functions that involve sine in terms of their rate of change.
The integral of the sine function is also crucial. The indefinite integral of sin(x) is:
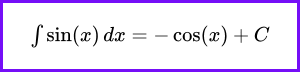
where C is the constant of integration. This integral is useful in various physical contexts, such as computing work done by variable forces or analyzing wave functions.
The sine function can be expressed as an infinite series, known as its Taylor series, centered at 0:

This series is particularly useful for approximating the values of the sine function for small angles (in radians) and in contexts where exact trigonometric values are not feasible.
The sine function frequently appears in solutions to differential equations, especially in physics, where it represents periodic motion. For example, the simple harmonic motion equation:

where ω and ϕ depend on initial conditions and system parameters.
In the context of Fourier series, the sine function is used to construct an orthogonal basis for periodic functions. Any reasonably well-behaved periodic function can be represented as an infinite sum of sines and cosines, which is fundamental in signal processing, heat transfer, and other fields.
The sine function is also essential in the evaluation of certain limits, a foundational concept in calculus. One famous limit is:
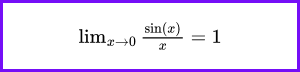
This limit is crucial for understanding small angle approximations and is used in the proofs of various other limits and calculus theorems.
The Law of Sines is a fundamental relationship in trigonometry that applies to any triangle. It relates the lengths of the sides of a triangle to the sines of its angles. This law is especially useful in solving problems where you need to find unknown sides or angles in a triangle, particularly in non-right triangles. Here’s how the Law of Sines is stated:
The Law of Sines states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is constant for all three sides and angles in a triangle. It can be written as:
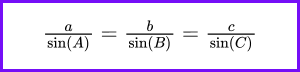
where a, b, and c are the lengths of the sides, and A, B, and C are the opposite angles of those sides, respectively.
This law is particularly useful in two scenarios:
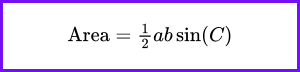
The inverse sine function, also known as arcsine, asin, or sin⁻¹, is crucial for calculating angles in right-angled triangles based on known side ratios. Represented as arcsine, this function helps determine the angle opposite a given side.
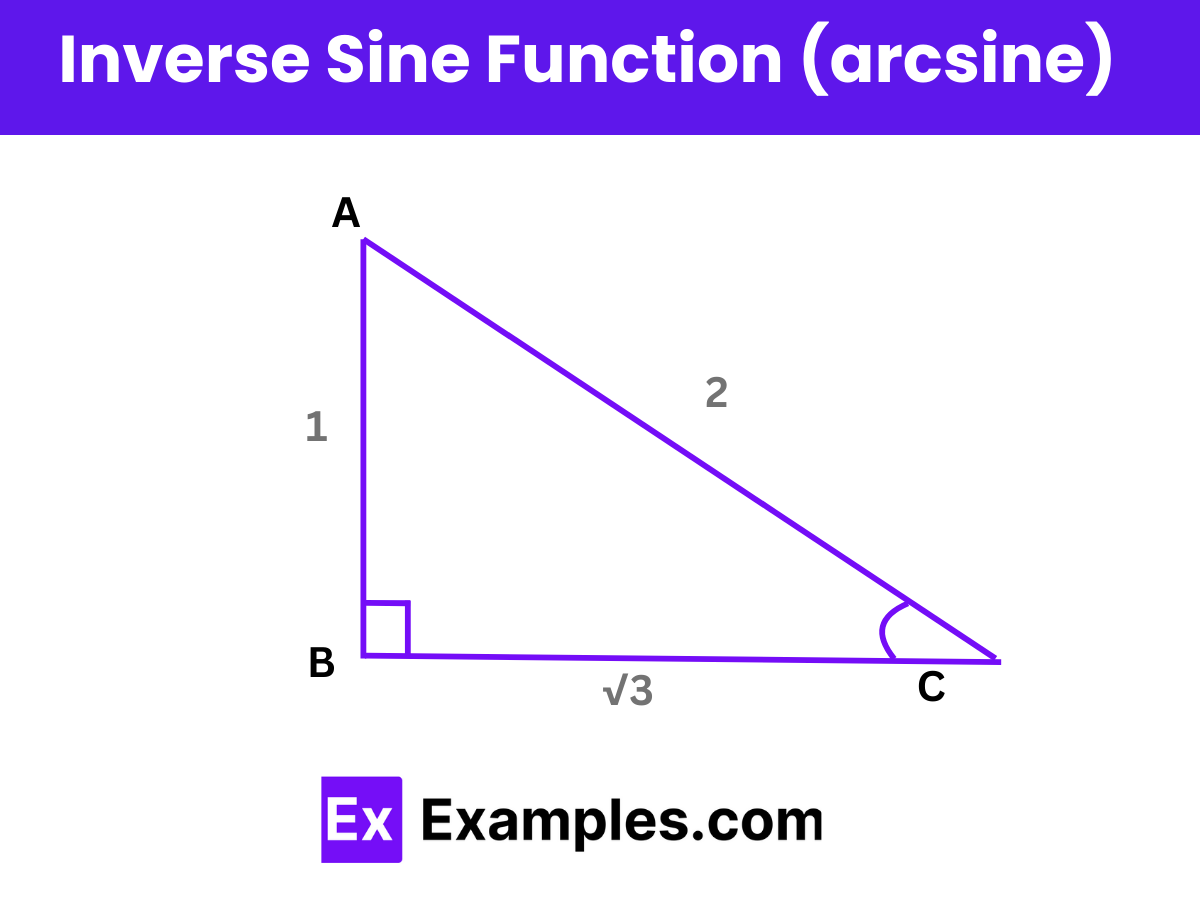
Consider a right triangle where the sides measure 1, 2, and √3. To find angle A, you can use the sine function, defined as the ratio of the opposite side to the hypotenuse:
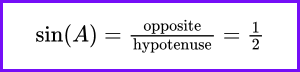
To find angle A, apply the arcsine function:

Suppose you know the angle of elevation to the top of a building is 30° and you are standing 100 meters away from the base of the building. You can calculate the height of the building using the sine function:
sin(30°)=opposite/hypotenuse=height of the building/100
height of the building=100×sin(30°)=100×1/2=50 meters
In engineering, the sine function is used to model periodic phenomena such as sound waves. If a sound wave can be modeled by the function:
y=sin(t)
where t is time, this equation describes how the displacement y from a rest position varies over time, depicting a pure tone.
In physics, simple harmonic motion can be modeled using the sine function, particularly for systems like a mass on a spring or a simple pendulum (under small angular displacements). The position x of the mass can be given as:
x(t)=Asin(ωt+ϕ)
where:
In circular motion, the coordinates of a point on the circumference of a circle can be described using sine and cosine functions. If the circle has radius rrr and the point makes an angle θ\thetaθ with the horizontal axis, the y-coordinate of the point is given by:
y=rsin(θ)
Sine functions are also integral in navigation for calculating distances across the Earth’s surface or determining the angle of the sun above the horizon, which can be crucial for celestial navigation.
To calculate sine, use the formula sin(θ)= opposite side / hypotenusein a right triangle, or look up the value in a trigonometric table or a calculator for non-triangular contexts.
The sine method in math refers to using the sine function to solve problems involving triangle measurements, wave functions, and periodic phenomena.
The term “sine” comes from the Latin word “sinus,” which means “bay” or “curve.” It was originally adopted from the Arabic translation of the Sanskrit term “jya-ardha” (half-chord).
The sine of 45 degrees is √2/2, which is derived from the properties of an isosceles right triangle where both angles are 45 degrees.
In trigonometry, find sin (sine) by dividing the length of the side opposite the angle by the length of the hypotenuse in a right-angled triangle.
For beginners, sine is a trigonometric function that helps determine the ratio of the opposite side to the hypotenuse of a right-angled triangle, crucial in calculating angles and distances.
The sine rule, easy explained, is a formula that helps solve any triangle by relating its sides with the sines of its angles: a/sinAa=b/sinB=c/sinC.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the sine of 30 degrees?
0.5
0.6
0.7
0.8
Which of the following is the sine of 90 degrees?
0
0.5
1
2
What is the sine of 45 degrees?
0.5
0.707
0.866
1
What is the sine of 30 degrees?
0.5
0.6
0.7
0.8
Which of the following angles has a sine value of 1?
60 degrees
90 degrees
45 degrees
30 degrees
What is the sine of 0 degrees?
0
0.5
1
- 1
What is the sine of 180 degrees?
-1
1
0.5
0
If sin θ = 0.8, what is θ in degrees if it is in the first quadrant?
53 degrees
60 degrees
30 degrees
45 degrees
What is the sine of 270 degrees?
0
0.5
1
-1
Which angle has a sine value of √3/2?
30 degrees
45 degrees
60 degrees
90 degrees
Before you leave, take our quick quiz to enhance your learning!

