What is the GCF of 16 and 28 multiplied by 3?
9
10
11
12
of 10
GCF of 16 and 28
GCF of 16 and 28
The Greatest Common Factor (GCF) of 16 and 28 is determined by finding the largest factor that both numbers share. First, list the factors of each number: for 16, the factors are 1, 2, 4, 8, and 16, while for 28, the factors are 1, 2, 4, 7, 14, and 28. The common factors are 1, 2, and 4. The largest of these common factors is 4. Therefore, the GCF of 16 and 28 is 4, which is useful for simplifying fractions and solving various mathematical problems involving these numbers.
GCF of 16 and 28
GCF of 16 and 28 is 4.
Methods to Find GCF of 16 and 28
- Prime Factorization Method
- Long Division Method
- Listing Common Factors
GCF of 16 and 28 by Prime Factorization Method.
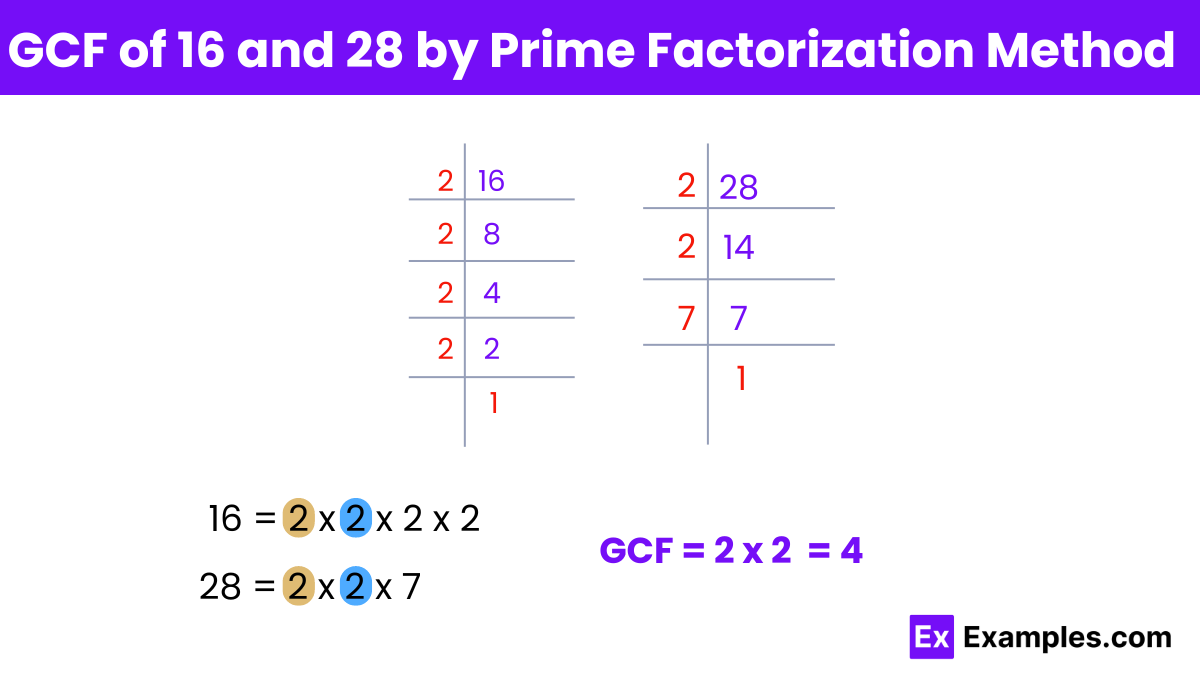
Prime Factorization of Each Number:
Prime factors of 16:
16 = 2 × 2 × 2 × 2
16 = 2⁴
Prime factors of 28:
28 = 2 × 2 × 7
28 = 2² × 7
Identify the Common Prime Factors:
- The common prime factor is 2.
- The lowest power of the common prime factor is 2².
Multiply the Common Prime Factors:
GCF = 2²
GCF = 4
GCF of 16 and 28 by Long Division Method.
Step-by-Step Process:
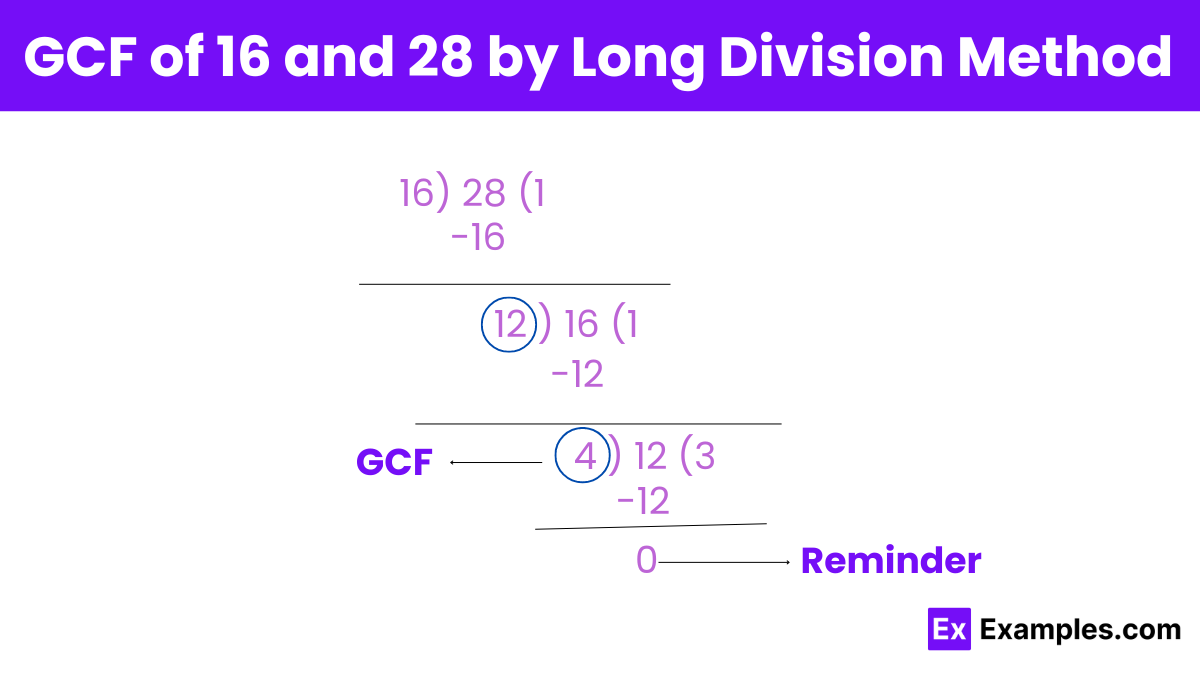
Divide the Larger Number by the Smaller Number:
Divide 28 (larger number) by 16 (smaller number).
28 ÷ 16 = 1 remainder 12
Replace the Larger Number with the Smaller Number:
The divisor (16) becomes the new dividend.
The remainder (12) becomes the new divisor.
Repeat the Division:
Now, divide 16 by 12.
16 ÷ 12 = 1 remainder 4
Repeat the Division Again:
Now, divide 12 by 4.
12 ÷ 4 = 3 remainder 0
Check the Remainder:
When the remainder is 0, the current divisors is the GCF.
The remainder is 0, and the current divisor is 4.
GCF of 16 and 28 by Listing Common Factors.
Step-by-Step Process:
List the Factors of Each Number:
Factors of 16: 1, 2, 4, 8, 16
Factors of 28: 1, 2, 4, 7, 14, 28
Identify the Common Factors:
The common factors of 16 and 28 are: 1, 2, 4
Find the Greatest Common Factor:
The largest number in the list of common factors is 4.
What is the GCF of 16 and 28?
The GCF of 16 and 28 is 4.
Can the GCF of 16 and 28 be found using the Euclidean algorithm?
Yes, the Euclidean algorithm involves repeated division. Divide 28 by 16, get the remainder 12. Then, divide 16 by 12, get the remainder 4. Finally, divide 12 by 4 to get a remainder of 0. The GCF is 4.
Is the GCF of 16 and 28 the same as their highest common factor?
Yes, the Greatest Common Factor (GCF) and the Highest Common Factor (HCF) are the same, which is 4 for 16 and 28.
What are the applications of GCF in everyday life?
GCF is used in various applications such as optimizing resources, organizing events, dividing assets, and simplifying ratios.
How is the GCF used in solving ratio problems?
The GCF is used to simplify ratios. For example, the ratio 16:28 simplifies to 4:7 by dividing both terms by their GCF, which is 4.
Can the GCF of 16 and 28 be used in solving Diophantine equations?
Yes, the GCF is used in solving Diophantine equations, which are equations with integer solutions. Knowing the GCF helps determine if a solution exists and simplifies the process of finding solutions.
Share :
Practice Test
What is the result of dividing the GCF of 16 and 28 by 2?
1
2
3
4
of 10
What is the GCF of 16, 28, and 40?
4
8
12
20
of 10
The GCF of 16 and 28 is subtracted from 16. What is the result?
8
12
14
20
of 10
What is the difference between the GCF of 16 and 28 and the number 3?
1
2
3
4
of 10
Which of the following numbers is not divisible by the GCF of 16 and 28?
12
20
24
26
of 10
The GCF of 16 and 28 is what fraction of 16?
1/2
1/4
1/3
1/8
of 10
. What is the GCF of 16 and 28 when divided by 4?
1
2
3
4
of 10
What is the GCF of 16 and 28?
2
4
8
12
of 10
Which of these is a factor of both 16 and 28?
6
7
4
5
of 10