GCF of 18 and 24
GCF of 18 and 24
The Greatest Common Factor (GCF) of 18 and 24 is the highest number that can evenly divide both 18 and 24 without leaving a remainder. Understanding the concept of the GCF, also known as the Greatest Common Divisor (GCD), is essential in mathematics, especially in number theory and algebra. The factors of 18 include 1, 2, 3, 6, 9, and 18, while the factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24. The GCF is a foundational concept that helps simplify fractions, solve equations, and understand relationships between numbers. By using the prime factorization method, we find the common prime factors of 18 (2 × 3 × 3) and 24 (2 × 2 × 2 × 3), identifying the GCF as 6. used: the long division method, the prime factorization method, and the Euclidean algorithm.
GCF of 18 and 24
GCF of 18 and 24 is 6.
The Greatest Common Factor (GCF) of 18 and 24 is 6. The simplest way to find it is by listing the factors of each number. The factors of 18 are 1, 2, 3, 6, 9, and 18; the factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24. The largest common factor is 6.
Methods to Find GCF of 18 and 24
- Prime Factorization Method
- Long Division Method
- Listing Common Factors
GCF of 18 and 24 by Prime Factorization Method
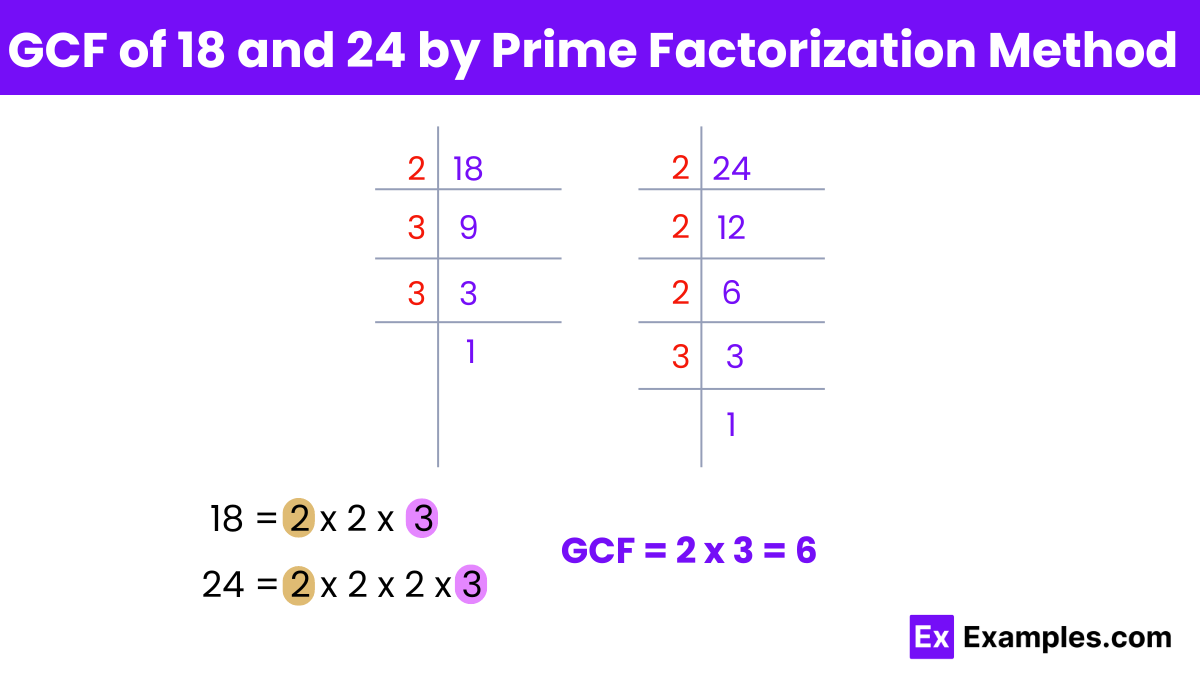
The prime factorization of 18 and 24 is (2 × 3 × 3) and (2 × 2 × 2 × 3) respectively. As visible, 18 and 24 have common prime factors. Hence, the HCF (Highest Common Factor) of 18 and 24 is 2 × 3 = 6.
HCF of 18 and 24 by Long Division:
- The HCF of 18 and 24 is the divisor we get when the remainder becomes 0 after repeatedly performing long division.
Steps:
- Divide 24 (larger number) by 18 (smaller number).
- Since the remainder is not 0, divide the divisor of step 1 (18) by the remainder (6).
- Repeat this process until the remainder is 0.
The corresponding divisor (6) is the HCF of 18 and 24.
GCF of 18 and 24 by Long Division Method.
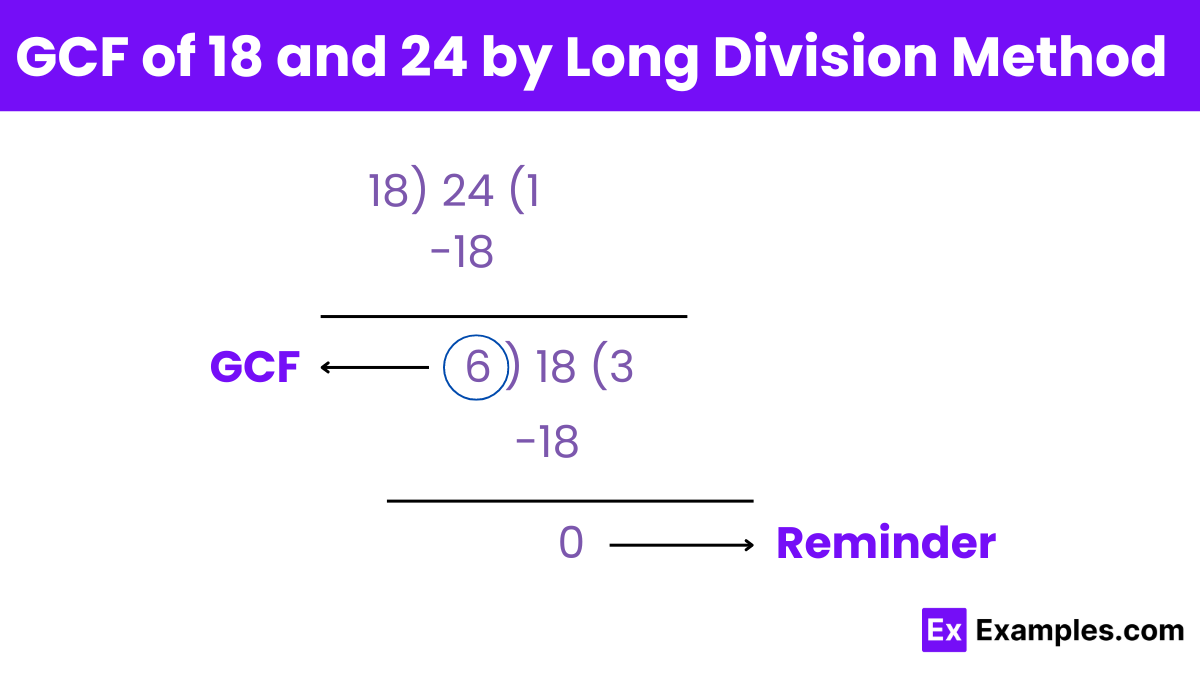
The GCF of 18 and 24 can be found using the long division method by following these steps:
Step 1: Divide 24 (the larger number) by 18 (the smaller number).
- Calculation: 24 ÷ 18 = 1 with a remainder of 6.
24 ÷ 18 = 1 remainder 6
Step 2: Use the divisor (18) from Step 1 and divide it by the remainder (6).
- Calculation: 18 ÷ 6 = 3 with a remainder of 0.
18 ÷ 6 = 3 remainder 0
Step 3: When the remainder becomes 0, the divisor at this step (6) is the GCF. The corresponding divisor, 6, is the GCF of 18 and 24.
GCF of 18 and 24 by Listing Common Factors
To find the GCF (Greatest Common Factor) of 18 and 24 by listing common factors, follow these steps:
List the factors of 18:
Factors of 18: 1, 2, 3, 6, 9, 18
List the factors of 24:
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Identify the common factors:
Common factors of 18 and 24: 1, 2, 3, 6
Determine the greatest common factor:
The greatest common factor among these is 6.
Thus, the GCF of 18 and 24 is 6.
What is the LCM of 18 and 24 by prime factorization method?
The LCM of 18 and 24 by prime factorization is found by multiplying the highest powers of all prime factors: 2³ ×3 = 72². Thus, LCM = 72.
What is a factor of 24 and 18?
A factor of both 24 and 18 is a number that evenly divides both without leaving a remainder. Common factors include 1, 2, 3, and 6.
What are the multiples of 18 and 24?
Multiples of 18 include 18, 36, 54, 72, and 90. Multiples of 24 include 24, 48, 72, 96, and 120. Common multiples include 72 and 144.
Why is finding the GCF important?
The GCF is used to simplify fractions, solve problems involving ratios, and find common denominators in algebra.
Can the GCF of 18 and 24 be greater than 6?
No, the GCF of 18 and 24 cannot be greater than 6 because 6 is the largest number that can evenly divide both 18 and 24 without leaving a remainder.
Share :
