What is the Greatest Common Factor (GCF) of 18 and 27?
2
3
6
9


To determine the greatest common factor (GCF) of 18 and 27, various methods can be employed. One method is by listing common factors: for 18, the factors are 1, 2, 3, 6, 9, and 18, while for 27, they are 1, 3, 9, and 27. Among these, the largest common factor is 9. Another method is prime factorization: breaking down 18 into 2×3×3 and 27 into 3×3×3, the common prime factor is 3×3=9. Thus, regardless of the method used, the GCF of 18 and 27 remains 9, signifying the largest numbers that divides both without leaving a remainder.
The greatest common factor (GCF) of 18 and 27 is 9. By listing common factors or prime factorization, 9 emerges as the largest number dividing both without remainder.
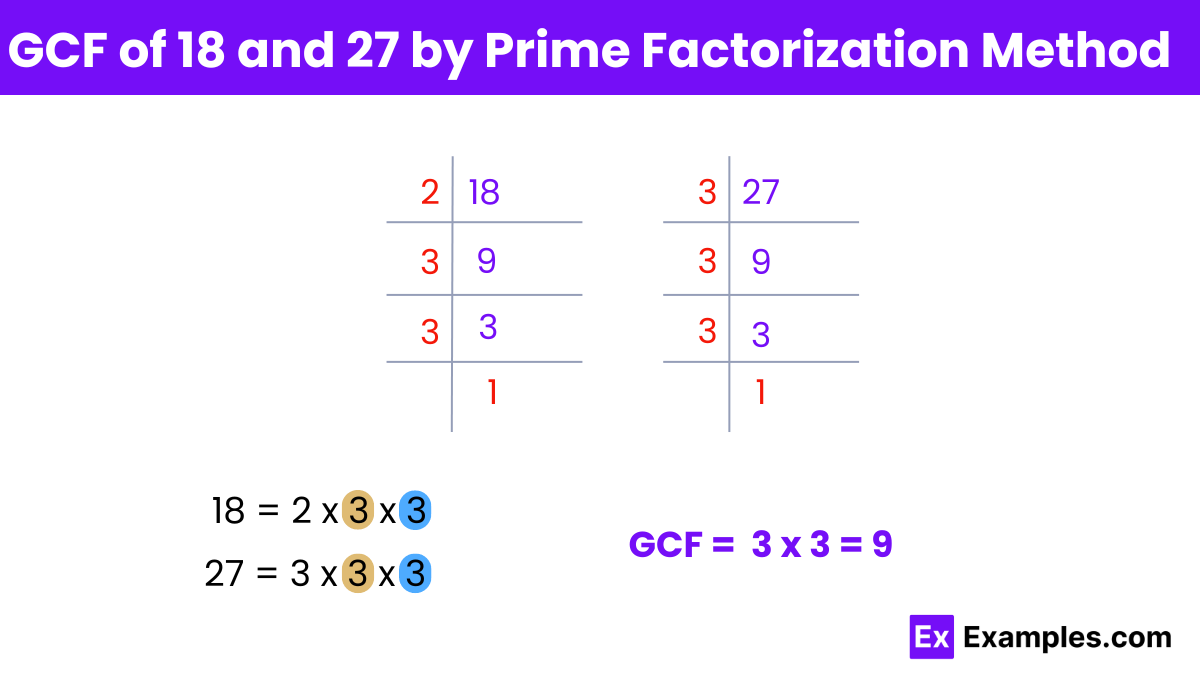
Find the prime factors of each number:
Prime factors of 18:
Divide 18 by 2 (the smallest prime number):18 ÷ 2 =9.
Next, factorize 9, which is not a prime number:9 ÷ 3 = 3.
Therefore, the prime factors of 18 are:18 = 2 × 3 × 3 or 2 × 3²
Prime factors of 27:
Divide 27 by 3 (the smallest prime number):27 ÷ 3 = 9.
Next, factorize 9, which is not a prime number:9 ÷ 3 = 3.
Therefore, the prime factors of 27 are:27 = 3 × 3 × 3 or 3³
Identify the common prime factors:
The prime factors of 18 are 2×3².
The prime factors of 27 are 3³.
The common prime factor is 3, and the smallest power of 3 in both factorizations is 3².
Multiply the common prime factors:
The GCF is found by multiplying the common prime factors with the smallest exponents :
GCF = 3² = 9
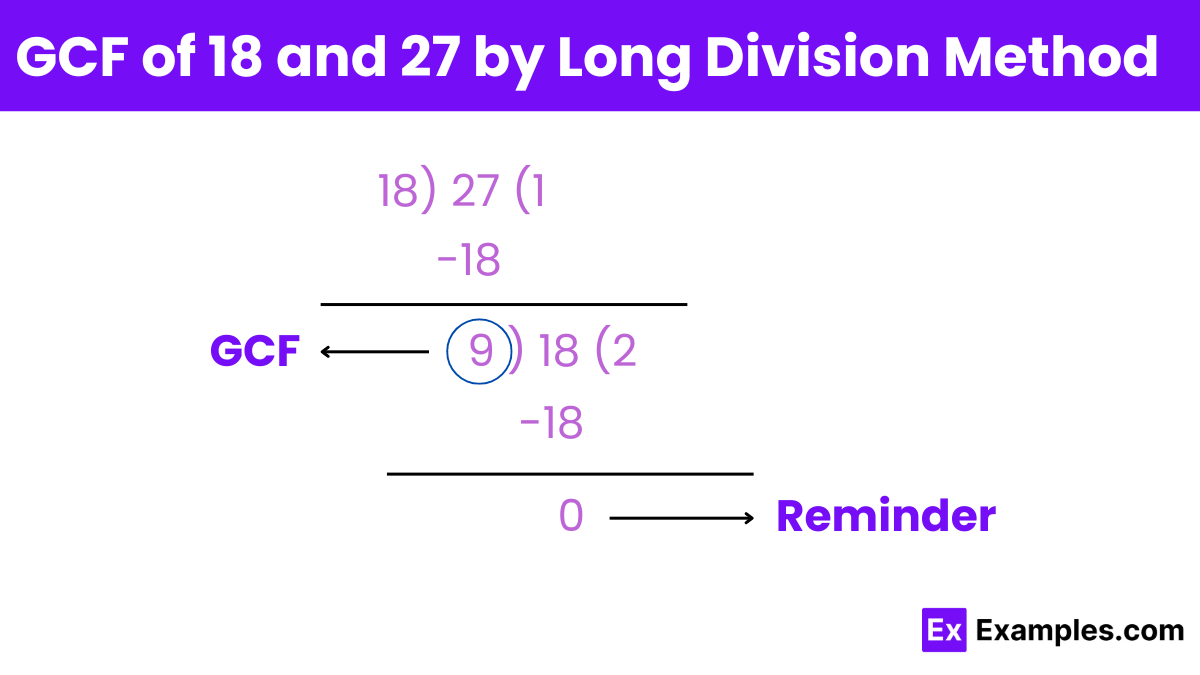
Divide the larger number by the smaller number:
27 ÷ 18 = 1 (quotient) , remainder = 27 − (18×1) = 9
Replace the larger number with the smaller number and the smaller number with the remainder:
Divide the new larger number by the new smaller number:
18 ÷ 9 = 2 (quotient ), remainder = 18 − (9×2) = 0
Repeat the process until the remainder is 0:
The divisor at this step is the GCF:
The divisor at the last step before the remainder became 0 is 9.

List the factors of each number:
Factors of 18: 1, 2, 3, 6, 9, 18
Factors of 27: 1, 3, 9, 27
Identify the common factors:
The common factors of 18 and 27 are: 1, 3, 9
Determine the greatest common factor:
The GCF is useful for simplifying fractions, dividing quantities evenly, and solving problems involving ratios.
No, the GCF cannot be larger than the smallest of the given numbers.
Understanding GCF helps students simplify fractions, solve problems involving divisors, and enhance their number theory skills.
The GCF can be used for reducing fractions, dividing items into equal groups, and solving problems in finance, engineering, and computer science.
Yes, the GCF can be found for negative numbers. The GCF of -18 and 27 is the same as the GCF of 18 and 27, which is 9. The GCF is always a positive number.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the Greatest Common Factor (GCF) of 18 and 27?
2
3
6
9
Which of the following is a common factor of both 18 and 27?
2
5
9
12
The product of the GCF of 18 and 27 and the GCF of 27 and 36 is:
27
36
45
81
The GCF of 18 and 27 is one-third of which of the following numbers?
9
12
18
27
Which of the following statements is true about the GCF of 18 and 27?
It is a factor of 18.
It is an even number.
It is a prime number.
It is a multiple of 4.
What is the difference between the LCM and GCF of 18 and 27?
45
54
63
72
The GCF of 18 and 27 is also the GCF of which of the following pairs?
12 and 36
18 and 36
27 and 45
18 and 54
If the GCF of 18 and 27 is multiplied by the largest factor of 18, what is the result?
54
72
81
108
What is the GCF of 18 and 27, if 18 is divided by its smallest prime factor?
2
3
6
9
What is the GCF of 2 times 18 and 2 times 27?
9
12
18
36
Before you leave, take our quick quiz to enhance your learning!

