GCF of 24 and 32
GCF of 24 and 32
The Greatest Common Factor (GCF) of 24 and 32 is determined by finding the largest factor that both numbers share. First, list the factors of each number: for 24, the factors are 1, 2, 3, 4, 6, 8, 12, and 24, while for 32, the factors are 1, 2, 4, 8, 16, and 32. The common factors are 1, 2, 4, and 8. The largest of these common factors is 8. Therefore, the GCF of 24 and 32 is 8.
GCF of 24 and 32
GCF of 24 and 32 is 8.
Methods to Find GCF of 24 and 32
- Prime Factorization Method
- Long Division Method
- Listing Common Factors
GCF of 24 and 32 by Prime Factorization Method.
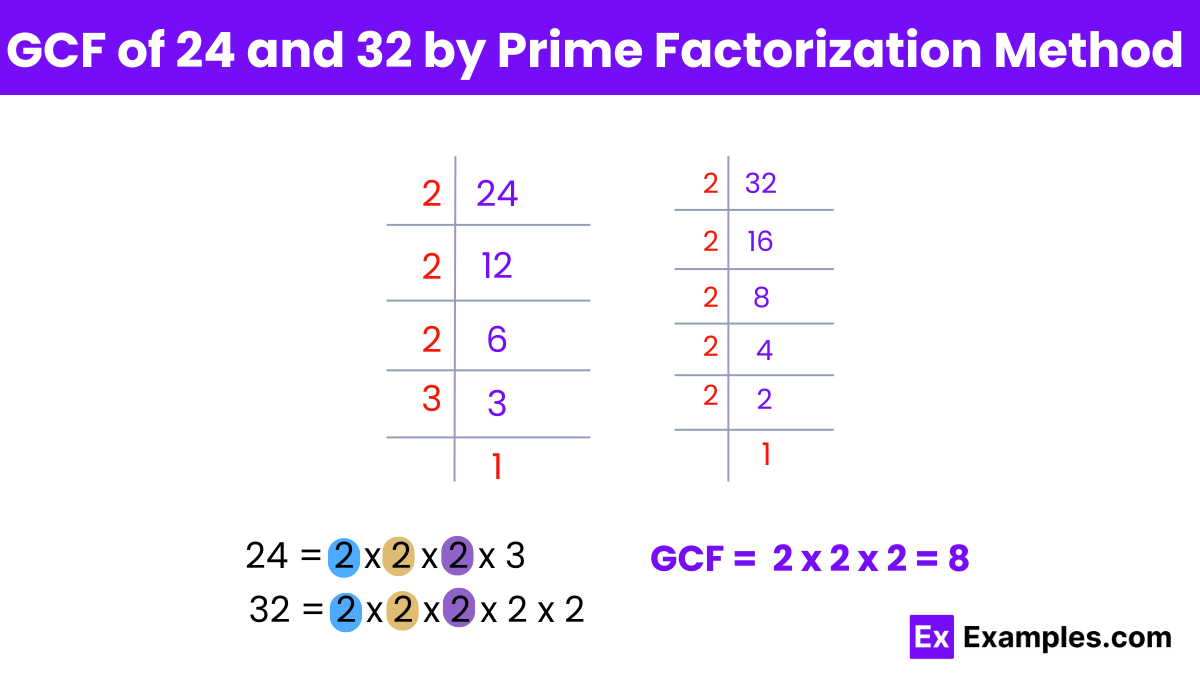
To find the Greatest Common Factor (GCF) of 24 and 32 using the prime factorization method, follow these steps:
Step-by-Step Process:
Prime Factorization of Each Number:
Prime factors of 24:
24 = 2 × 2 × 2 × 3
24 = 2³ × 3
Prime factors of 32:
32 = 2 × 2 × 2 × 2 × 2
32 = 2⁵
Identify the Common Prime Factors:
The common prime factor is 2.
The lowest power of the common prime factor is 2³.
Multiply the Common Prime Factors:
GCF = 2³
GCF = 8
GCF of 24 and 32 by Long Division Method.
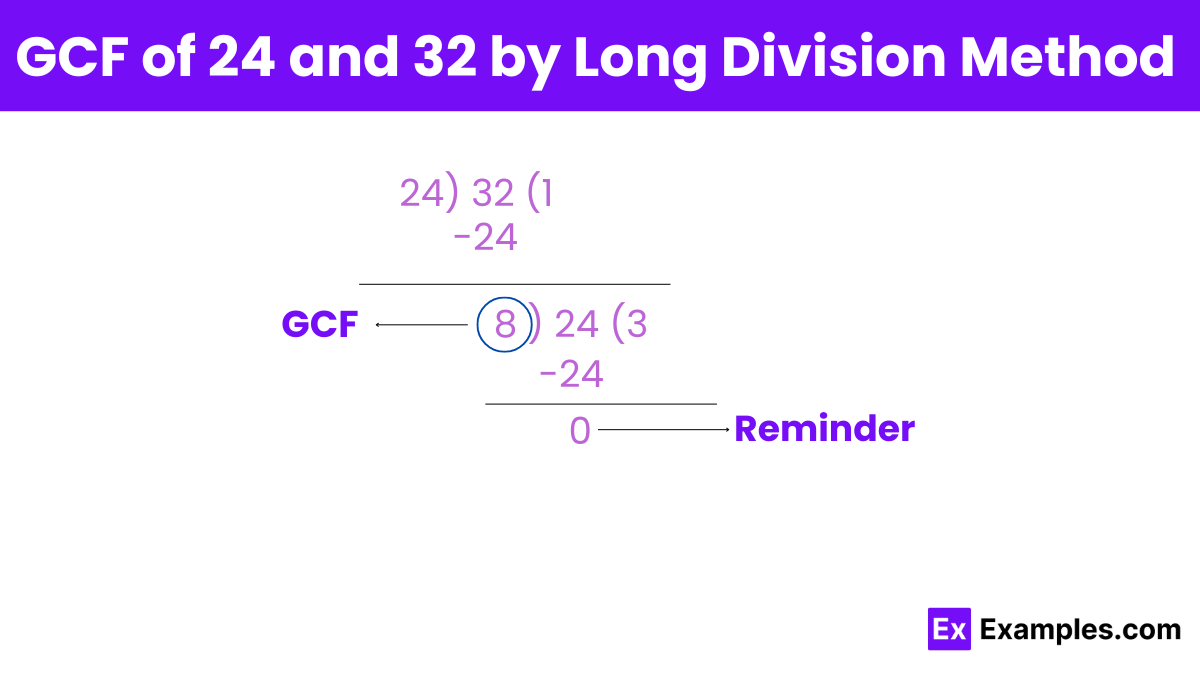
Divide the Larger Number by the Smaller Number:
Divide 32 (larger number) by 24 (smaller number).
32 ÷ 24 = 1 remainder 8
Replace the Larger Number with the Smaller Number:
The divisor (24) becomes the new dividend.
The remainder (8) becomes the new divisor.
Repeat the Division:
Now, divide 24 by 8.
24 ÷ 8 = 3 remainder 0
Check the Remainder:
When the remainder is 0, the current divisors is the GCF.
The remainder is 0, and the current divisor is 8.
GCF of 24 and 32 by Listing Common Factors.
List the Factors of Each Number:
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
- Factors of 32: 1, 2, 4, 8, 16, 32
Identify the Common Factors:
- The common factors of 24 and 32 are: 1, 2, 4, 8
Find the Greatest Common Factor:
The largest number in the list of common factors is 8.
What is the GCF and LCM of 24 and 32?
The Greatest Common Factor (GCF) of 24 and 32 is 8, and the Least Common Multiple (LCM) of 24 and 32 is 96. These values are crucial for simplifying fractions and solving ratio problems.
What is the greatest GCF of 24 and 32?
The greatest GCF of 24 and 32 is 8. This value represents the largest factor that both numbers share, essential for simplifying fractions and solving various mathematical problems.
Can the GCF of 24 and 32 be found using the Euclidean algorithm?
Yes, the Euclidean algorithm involves repeated division. Divide 32 by 24, get the remainder 8, then divide 24 by 8 to get a remainder of 0. The GCF is 8.
How can finding the GCF of 24 and 32 help in real-life problems?
It helps in tasks such as simplifying recipes, splitting objects into equal parts, and solving problems involving proportions or ratios.
How does the GCF help in simplifying fractions involving 24 and 32?
The GCF helps reduce fractions to their simplest form. For example, 24/32 simplifies to 3/4 when both numerator and denominator are divided by their GCF, which is 8.
How is the GCF used in solving ratio problems?
The GCF is used to simplify ratios. For example, the ratio 24:32 simplifies to 3:4 by dividing both terms by their GCF, which is 8.
Share :
