What is the Greatest Common Factor (GCF) of 35 and 50?
5
7
10
15


The Greatest Common Factor (GCF) of 35 and 50 is 5. This is determined by identifying the common prime factors of the two numbers. The prime factorization of 35 is 5 × 7, and the prime factorization of 50 is 2 × 5 × 5. The only common prime factor is 5, making it the GCF of 35 and 50.
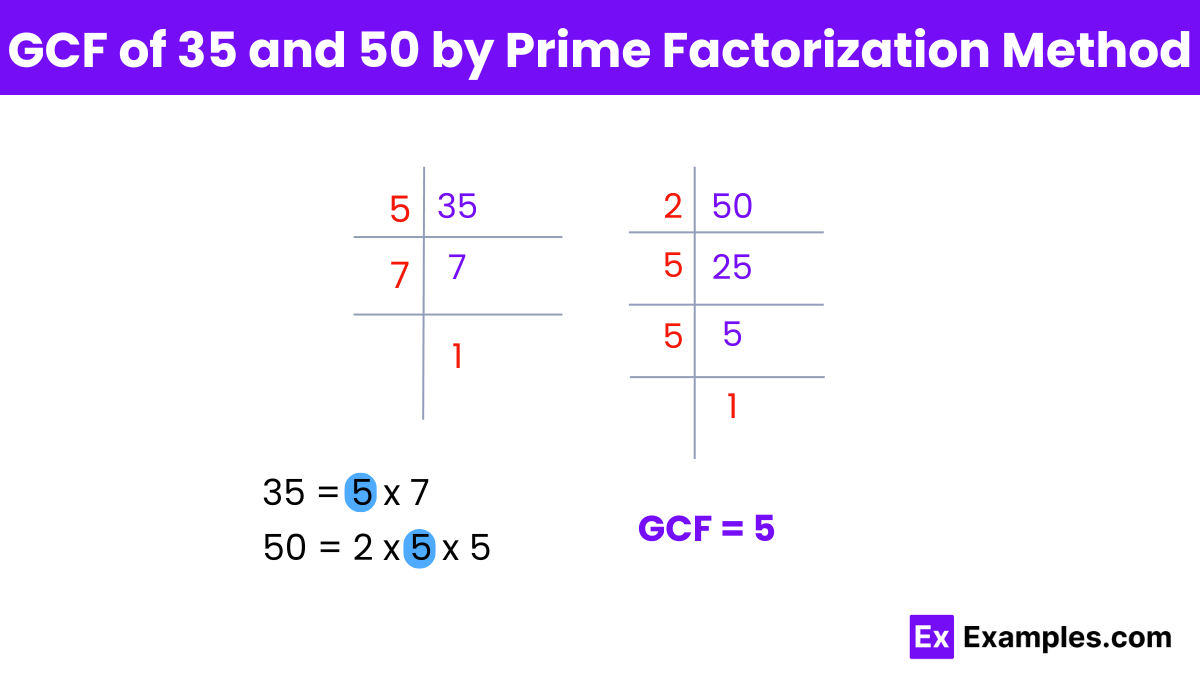
Prime Factorization of 35:
Prime Factorization of 50:
Identify Common Factors:
Determine the GCF:
Since the only common prime factor is 5, the GCF of 35 and 50 is 5.
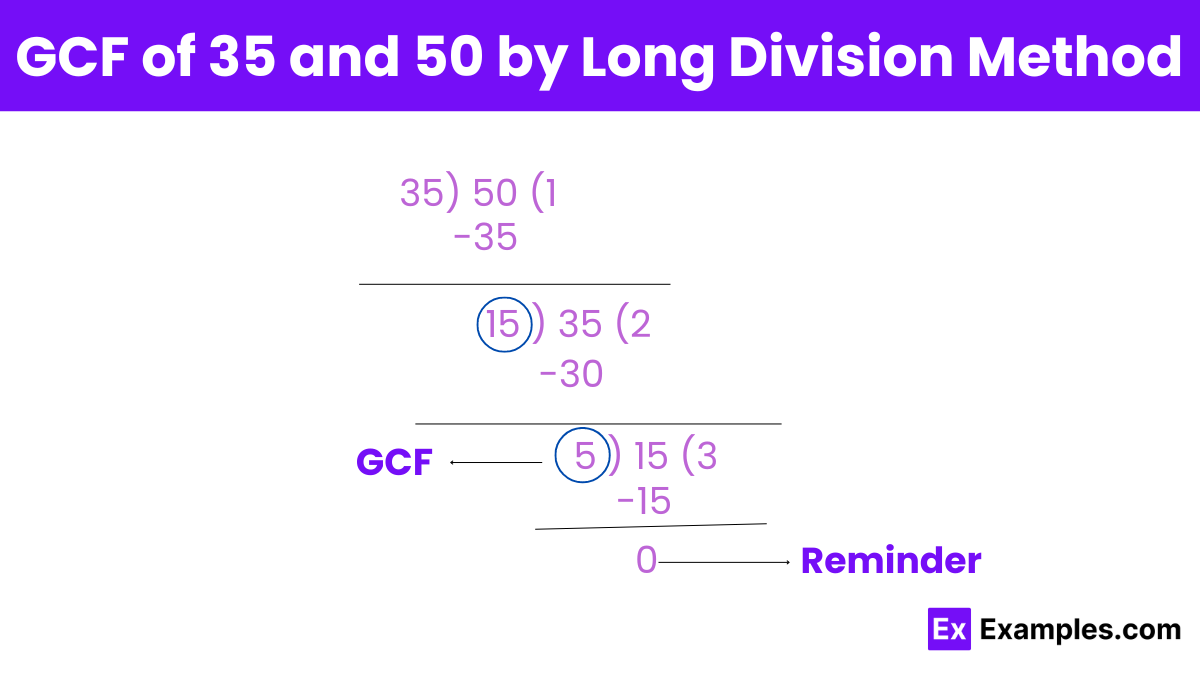
Divide the larger number (50) by the smaller number (35):
50 ÷ 35 gives a quotient of 1 and a remainder of 15.
Replace the larger number with the smaller number (35) and the smaller number with the remainder (15):
Now, divide 35 by 15.
35 ÷ 15 gives a quotient of 2 and a remainder of 5.
Repeat the process: Replace 35 with 15 and 15 with the remainder 5.
Now, divide 15 by 5.
15 ÷ 5 gives a quotient of 3 and a remainder of 0.
When the remainder is 0, the divisors at this step is the GCF.
So, the GCF of 35 and 50 is 5.

List the factors of 35:
Factors of 35: 1, 5, 7, 35
List the factors of 50:
Factors of 50: 1, 2, 5, 10, 25, 50
Identify the common factors:
Common factors of 35 and 50: 1, 5
Determine the greatest common factor:
The greatest common factor is 5.
Therefore, the GCF of 35 and 50 is 5.
The GCF (Greatest Common Factor) of 35 and 50 is 5.
The GCF is important in simplifying fractions, solving problems involving ratios, and finding common denominators.
No, the GCF of 35 and 50 cannot be greater than 5 because 5 is the largest number that divides both 35 and 50 without leaving a remainder.
The GCF is used in real-life situations such as dividing items into smaller sections, comparing quantities, and simplifying mathematical problems involving fractions.
Yes, many calculators have a function to find the GCF of two numbers. Simply input the numbers 35 and 50 and use the GCF or GCD function.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the Greatest Common Factor (GCF) of 35 and 50?
5
7
10
15
Which number is a common factor of both 35 and 50?
2
5
7
10
How many common factors do 35 and 50 have?
1
2
3
4
What is the smallest common factor of 35 and 50?
1
5
7
10
Which of the following is not a common factor of 35 and 50?
1
5
7
10
The GCF of 35 and 50 is also a factor of which of the following numbers?
5
35
50
All of the above
If you multiply the GCF of 35 and 50 by 3, what do you get?
10
15
20
30
Which of the following pairs of numbers has the same GCF as 35 and 50?
30 and 45
50 and 70
35 and 60
70 and 85
What is the GCF of 35, 50, and 70?
5
10
15
20
The sum of the GCF of 35 and 50 and the smallest prime number is:
6
7
8
9
Before you leave, take our quick quiz to enhance your learning!

