GCF of 48 and 64
GCF of 48 and 64
The Greatest Common Factor (GCF) of 48 and 64 is 16. To find the GCF, we list the prime factors of both numbers. The prime factors of 48 are 2 × 2 × 2 × 2 × 3 (or (2⁴ × 3)), and the prime factors of 64 are 2 × 2 × 2 × 2 × 2 × 2 (or (2⁶)). The common prime factor is 2, and the highest power of 2 that is common to both numbers is (2⁴). Therefore, the GCF is (2⁴) which equals 16.
GCF of 48 and 64
GCF of 48 and 64 is 16.
Methods to Find GCF of 48 and 64
- Prime Factorization Method
- Long Division Method
- Listing Common Factors
GCF of 48 and 64 by Prime Factorization Method.
Step 1: Find the prime factors of each number.
Prime factors of 48: 2 x 2 x 2 x 2 x 3
Prime factors of 64: 2 x 2 x 2 x 2 x 2 x 2
Step 2: Identify the common prime factors.
- Common prime factors: 2 x 2 x 2 x 2 = (2⁴)
Step 3: Multiply the common prime factors.
GCF = (2⁴) = 16
So, the greatest common factor of 48 and 64 is 16.
GCF of 48 and 64 by Long Division Method.
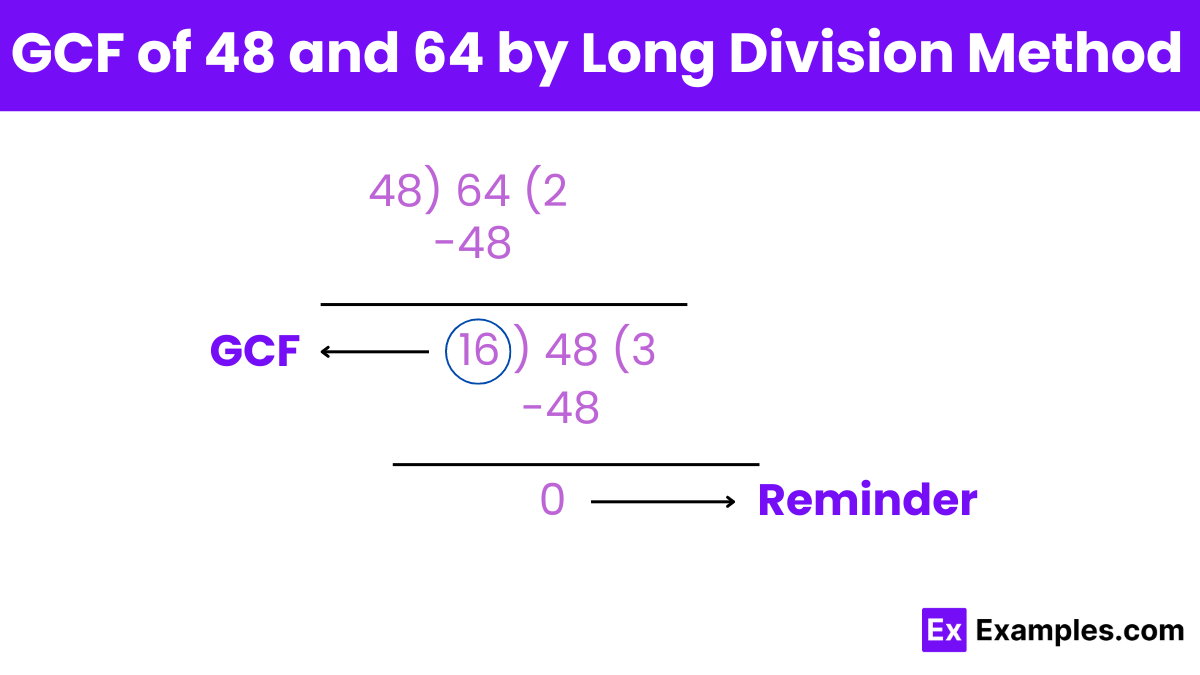
Step 1: Divide the larger number by the smaller number
64 ÷ 48 = 1 with a remainder of 16.
Step 2: Replace the larger number with the smaller number, and the smaller number with the remainder
Now, we have 48 and 16.
Step 3: Repeat the division
48 ÷ 16 = 3 with a remainder of 0.
Step 4: When the remainder is 0, the divisors is the GCF
The last non-zero remainder is 16. So, the GCF of 48 and 64 is 16.
GCF of 48 and 64 by Listing Common Factors.
To find the Greatest Common Factor (GCF) of 48 and 64 by listing common factors, follow these steps:
Step 1: List the factors of each number
Factors of 48:
- 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Factors of 64:
- 1, 2, 4, 8, 16, 32, 64
Step 2: Identify the common factors
Common factors of 48 and 64:
- 1, 2, 4, 8, 16
Step 3: Determine the greatest common factor
The largest common factor is 16. Therefore, the GCF of 48 and 64 is 16.
How do you find the GCF of 48 and 64?
You can find the GCF by using the long division method or by listing common factors.
Why is the GCF of 48 and 64 important?
The GCF is useful in simplifying fractions and solving problems involving divisibility.
Can the GCF of 48 and 64 be used to simplify the fraction 48/64?
Yes, simplifying 48/64 using the GCF of 16 gives 3/4.
How are the GCF and LCM of two numbers related?
The product of the GCF and LCM of two numbers equals the product of the numbers.
How do you verify the GCF using the Euclidean algorithm?
By repeatedly applying the division method until the remainder is zero.
Can you use the GCF to find the common factors of multiple numbers?
Yes, you can extend the method to find the GCF of more than two numbers.
Share :
