Square & Square Root of 4096
Square & Square Root of 4096
In the realm of algebraic mathematics, squares and square roots are foundational concepts of paramount importance. Squaring a number, as illustrated by the example of 4096, involves multiplying it by itself to yield 16777216, a fundamental operation. This process is key in exploring properties inherent in both rational (expressible as fractions) and irrational numbers (defying neat fraction expressions). Understanding these concepts enriches comprehension of mathematical relationships and patterns. Algebraic studies delve into these operations, revealing insights into the intricate interplay between numbers and their properties, fostering a deeper appreciation for the elegance and complexity of mathematical structures. Thus, mastery of these fundamental concepts forms a solid basis for further mathematical exploration and problem-solving endeavors.
Square of 4096
A square number, like 4096, is obtained by multiplying a number by itself. In this case, squaring 4096 results in 16777216. Square numbers are foundational in mathematics, serving as building blocks for understanding algebraic concepts and exploring the inherent properties of numbers within mathematical frameworks.
Square Root of 4096
The square root of 4096, a square number, equals 64. It represents the value that, when multiplied by itself, yields 4096. Understanding square roots illuminates mathematical principles, aiding in solving equations, and grasping geometric concepts. In this case, the square root of 4096 elucidates the relationship between squares and their roots.
Is the Square Root of 4096 Rational or Irrational?
The square root of 4096 is a rational number. This is because 4096 is a perfect square (64 squared), resulting in a whole number (64) when square rooted. Rational numbers can be expressed as fractions of integers, and the square root of 4096, being a perfect square, is such an example.
Rational number A rational number can be represented as a fraction of two integers, where the denominator is not zero. Examples include positive, negative, or zero values like 3/4, -5/2, 0, 1, -2, etc.
Example: For instance, 3/4 is rational because both 3 and 4 are integers, and the denominator isn’t zero.
Irrational Number: An irrational number, such as √2 or π, cannot be expressed as a fraction of two integers. Its decimal expansion neither terminates nor repeats, making it impossible to represent as a fraction.
Example: Consider √2; its decimal expansion (√2 ≈ 1.41421356…) doesn’t repeat or terminate, making it irrational.
Method to Find Value of Root 4096
To find the value of the square root of 4096, you can use various methods:
Mental Calculation: Recognize that 4096 is a perfect square of 64. So, the square root of 4096 is 64.
Prime Factorization: Express 4096 as a product of its prime factors: (4096 = 2¹²). Since the square root of a product is the product of the square roots of its factors, the square root of 4096 equals (2² = 64).
Calculator: Most calculators have a square root function. Simply input 4096 and press the square root button to get the result, which should be 64.
These methods offer different approaches, but they all lead to the same result: the square root of 4096 is 64.
Square Root of 4096 by Long Division Method
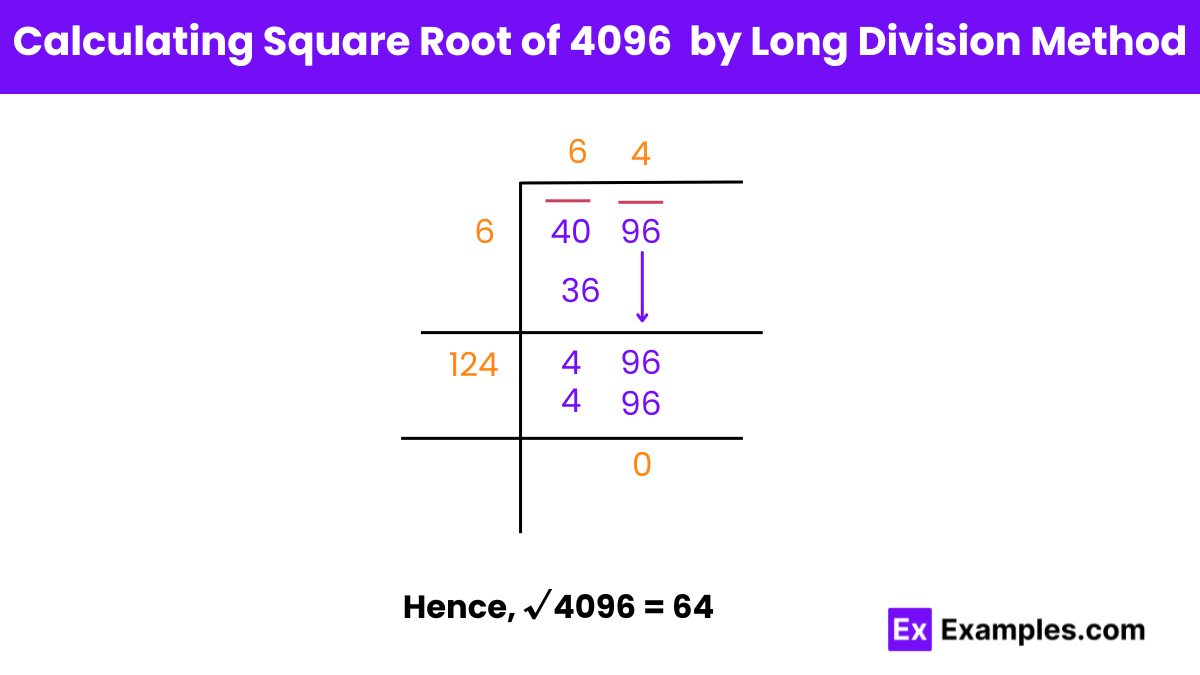
Forming Pairs:
Identify the pairs within the number to be square rooted. In this case, 4096 is broken down into pairs: 40 and 96.
Finding Y:
Determine a number Y (6 in this case) such that its square is less than or equal to the first pair, 40.
Division and Remainder:
Divide the first pair, 40, by Y (6), resulting in a quotient of 6 with a remainder of 4.
Bringing Down the Next Pair:
Move to the next pair, 96, placing it to the right of the remainder, 4, forming a new dividend, 496.
Updating the Divisor:
Add the last digit of the quotient (6) to itself, resulting in 12. Find a digit Z (4 in this case) such that 12Z multiplied by Z is less than or equal to 496.
Repeating the Division:
Form a new divisor, 124, using the updated divisor (12) and the found digit (4). Divide the new dividend, 496, by the new divisor, 124, yielding a quotient of 4 and a remainder of 0.
Completion:
Since the remainder is now 0 and there are no more digits to bring down, the process concludes. Therefore, the square root of 4096, determined by the long division method, is 64.
4096 is Perfect Square root or Not?
No, 4096 is not a perfect square number
Yes, 4096 is a perfect square because its square root, which is 64, is a whole number, indicating that 4096 is the result of multiplying an integer by itself.
FAQs
Why is 4096 considered a perfect square?
4096 is considered a perfect square because it is the result of multiplying an integer (64) by itself.
Can you explain the significance of the square root of 4096?
The square root of 4096 represents the side length of a square that has an area of 4096 square units. It’s also a fundamental concept in mathematics.
Are there any practical applications of knowing the square and square root of 4096?
Yes, understanding square roots is useful in various fields like geometry, physics, engineering, and computer science.
Is there a simplified form for the square root of 4096?
The square root of 4096 is already simplified as 64.
Can you provide step-by-step instructions for finding the square root of 4096?
Yes, you can use methods like prime factorization, a calculator, or long division to find the square root of 4096.
Share :
