Fourier Law – Examples, Definition, Formula, Derivation, FAQ’S

Fourier’s Law is a fundamental principle in the physics of heat transfer, stating that the rate of heat flow through a material is proportional to the negative gradient of the temperature and the area through which the heat is flowing. This law is crucial in understanding and predicting how heat moves through different mediums.

What is Fourier Law?

Fourier Law History

Fourier’s Law, a cornerstone in the field of thermodynamics, originates from the work of Jean-Baptiste Joseph Fourier, a French mathematician and physicist. His groundbreaking contributions revolutionized our understanding of heat transfer. Influencing not only physics but also engineering and other sciences.

Jean-Baptiste Joseph Fourier and His Discovery

Fourier introduced his law of heat conduction in the early 19th century, specifically in his seminal work “Théorie Analytique de la Chaleur” (The Analytical Theory of Heat) published in 1822. Through his research, Fourier aimed to describe the flow of heat in solid bodies, developing a theory that heat spreads through solid substrates via a diffusion process.

Development and Impact of Fourier’s Theory

Fourier’s assertion that the rate of heat transfer through a material. It is proportional to the negative gradient of the temperature field. It was initially met with skepticism. However, his mathematical treatments laid the foundation for what would become the heat equation. Fourier’s methods not only solved practical problems in heat conduction. But also introduced influential mathematical techniques. Such as Fourier series and Fourier transforms. Which are pivotal in various applications across multiple disciplines.

Types of Fourier Law

Fourier’s Law in One-Dimensional Heat Transfer

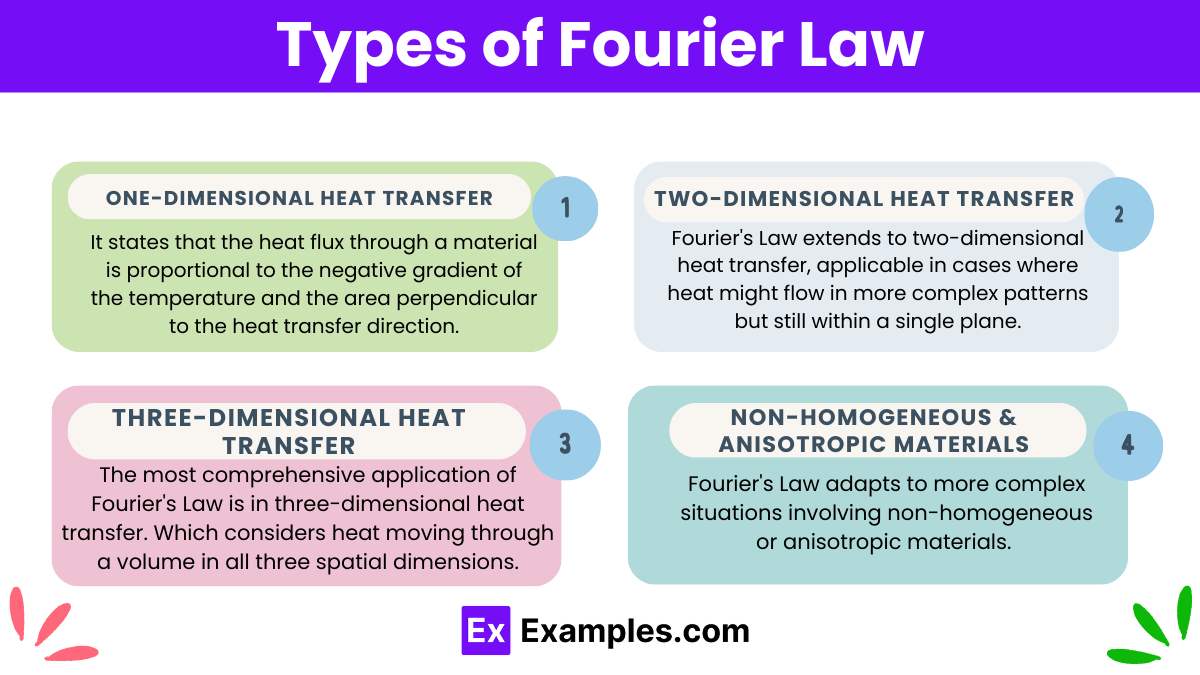
Firstly, we encounter Fourier’s Law in its simplest form in one-dimensional heat transfer scenarios. It states that the heat flux through a material is proportional to the negative gradient of the temperature and the area perpendicular to the heat transfer direction. Typically used in situations involving thin slabs or walls where heat flows in one direction, this formulation is a staple in introductory thermodynamics.

Fourier’s Law in Two-Dimensional Heat Transfer

Furthermore, Fourier’s Law extends to two-dimensional heat transfer, applicable in cases where heat might flow in more complex patterns but still within a single plane. Engineers often use this form when analyzing heat transfer across surfaces like building floors or walls, where the heat does not only move straightforwardly but might spread out across the plane of the material.

Fourier’s Law in Three-Dimensional Heat Transfer

Moreover, the most comprehensive application of Fourier’s Law is in three-dimensional heat transfer. Which considers heat moving through a volume in all three spatial dimensions. This variant is crucial for designing and analyzing systems where heat transfer is not limited to a single plane. Such as in large machinery, geological formations, or within biological tissues.

Fourier’s Law for Non-Homogeneous and Anisotropic Materials

Additionally, Fourier’s Law adapts to more complex situations involving non-homogeneous or anisotropic materials. In these cases, the thermal conductivity might vary with direction or position within the material. This adaptation allows for precise predictions and assessments in materials science and engineering, where materials may not uniformly conduct heat due to varying compositions or structured anisotropies.

Fourier Law Formula

Fourier’s Law is fundamental in the study of heat conduction, providing the basis for calculating how heat moves through materials. This law is particularly crucial for designing efficient thermal systems in engineering and understanding natural heat transfer processes in environmental sciences.

The Basic Formula

The formula for Fourier’s Law is expressed as:

where:

• 𝑞 represents the heat flux vector, which indicates the rate of heat transfer per unit area,
• 𝑘 is the thermal conductivity of the material, a measure of its ability to conduct heat,
• ∇𝑇 is the temperature gradient in the material.

Fourier Law Derivation

Fourier’s Law of Heat Conduction is a fundamental principle in thermodynamics that describes how heat transfers through materials. Here’s a step-by-step derivation of this important law:

Before deriving Fourier’s Law, it’s essential to understand some basic concepts in heat transfer:

• Heat Flux (𝑞): This is the rate at which heat energy flows through a unit area of a material, typically measured in watts per square meter (W/m²).
• Temperature Gradient (∇𝑇): This refers to the rate of change of temperature in space within a material, measured in degrees per meter (∘C/m or ∘K/m).

The derivation starts with the assumption that the heat flux vector (𝑞) is proportional to the local temperature gradient. This assumption is based on observational evidence in steady-state heat transfer (heat transfer at a constant rate over time).

Mathematical Expression

Here, 𝑘 represents the thermal conductivity of the material, a measure of its ability to conduct heat. The negative sign indicates that heat flows from higher to lower temperatures, following the second law of thermodynamics.

Heat Conduction Equation: By considering a differential control volume within the material, you can relate the heat flux to the rate of heat transfer through the material. For a steady-state one-dimensional case in a slab of material with cross-sectional area 𝐴 and thickness 𝑑𝑥, the rate of heat transfer (𝑄˙​) can be expressed as:

This equation means the heat flow rate is proportional to the thermal conductivity, the area through which the heat is flowing, and the temperature gradient across the thickness of the slab.

Generalization to Three Dimensions

Fourier’s Law can be extended to three dimensions by considering the vector nature of heat flux and temperature gradient:

In this form, 𝑞 and ∇𝑇 are vectors, and 𝑘 may be a scalar or a tensor if the material is anisotropic (i.e., its properties differ in different directions).

Differential Form of Fourier’s Law

To establish a relationship suitable for applying calculus, particularly in varying conditions such as non-uniform materials or temperatures that change over time, we integrate Fourier’s Law with the heat equation. The heat equation in its most general form combines Fourier’s Law with the conservation of energy principle:

Where:

• 𝑢 is the internal energy density of the material,
• ∂𝑢∂𝑡​ represents the rate of change of this energy density over time,
• 𝑞 represents internal heat generation per unit volume (such as heat generated by chemical reactions or electrical resistance).

Simplifying for Constant Thermal Conductivity

If the thermal conductivity 𝑘 is constant, which is often assumed for isotropic and homogeneous materials, the equation simplifies to:

Here, ∇²𝑇 (or Δ𝑇) is the Laplacian of the temperature. Which gives a measure of the rate at which the temperature field is diverging from any point in space.

Heat Equation in Energy Conservation Form

Considering the specific heat capacity (𝑐) and density (𝜌) of the material, the heat equation for heat conduction can be written as:

This form relates the change in temperature over time to the spatial distribution of temperature, material properties, and internal heat generation.

Fourier’s law in terms of conductance

To express Fourier’s Law in terms of thermal conductance, consider a simple case of one-dimensional heat flow through a homogeneous material with constant cross-sectional area and thermal conductivity. The formula then simplifies to:

Where:

• 𝑞 is the heat flow rate (in watts, W),
• Δ𝑇 is the temperature difference across the material (in degrees Celsius, °C or Kelvin, K),
• 𝐿 is the thickness of the material (in meters, m).

Uses of Fourier Law

• Engineering Design: Engineers use Fourier’s Law to calculate heat transfer rates in systems, ensuring that devices such as heat exchangers, radiators, and heat sinks are designed optimally for maximum efficiency.
• Building Insulation: In the construction industry, Fourier’s Law helps in designing buildings that maintain comfortable indoor temperatures. It is essential for selecting the right insulation materials that minimize heat loss in winter and reduce heat gain in summer.
• Climate Control Systems: This law is crucial for the development of effective heating, ventilation, and air conditioning (HVAC) systems. It allows for the precise calculation of heat flow, ensuring that environments remain at desired temperatures.
• Manufacturing Processes: Fourier’s Law is applied in various manufacturing processes that require precise temperature control. Such as in the curing of materials, chemical processing, and even in the cooking processes in food production.
• Thermal Management of Electronics: In the realm of electronics, managing the heat produced by devices is vital to ensure performance and longevity. Fourier’s Law guides the design of cooling systems in computers, smartphones, and other electronic devices.
• Geothermal Energy: The law is used to model geothermal heat transfer. Facilitating the exploration and development of geothermal energy resources, which are pivotal for sustainable energy solutions.

Examples for Fourier Law

• Thermal Insulation: In buildings, the effectiveness of insulation materials is analyzed using Fourier’s Law to prevent heat from escaping during winter and entering during summer. This helps maintain comfortable indoor temperatures and reduces energy costs.
• Cooking: The principle of heat conduction according to Fourier’s Law is critical in cooking processes. It explains how heat is transferred from the surface of a pan or oven to the center of the food, ensuring that it cooks evenly.
• Electronic Devices: Fourier’s Law is essential in designing cooling systems for electronic devices. Engineers use it to manage and dissipate the heat generated by electronic components. Thus preventing overheating and ensuring the devices operate within safe temperature ranges.
• Automotive Industry: The law helps in the design of automotive components, such as engine parts and brake systems, that need to effectively manage heat during operation to prevent failure and maintain performance.
• Refrigeration and Air Conditioning: Fourier’s Law is crucial in the design of heat exchangers used in refrigerators and air conditioners. It helps optimize how these systems transfer heat from one area to another. Enhancing efficiency and effectiveness.
• Medical Equipment: In medical science, Fourier’s Law is used in devices like MRI machines and other diagnostic tools that require precise temperature control to function correctly and safely.

FAQ’S

What is steady-state Fourier’s law?

Steady-state Fourier’s law describes heat conduction when the temperature gradient and heat flow rate remain constant over time, resulting in a stable thermal environment.

What is the Fourier’s law of radiation?

Fourier’s law of radiation isn’t a standard term; Fourier’s law specifically describes heat conduction, not radiation. Heat radiation follows Stefan-Boltzmann and Planck’s laws instead.

Why is the Fourier’s law important?

Fourier’s law is essential for calculating how heat transfers through materials, crucial for designing thermal systems in engineering, building insulation, and various technological applications.