Learning Objectives
In studying Introduction to Solubility Equilibria for the AP Chemistry exam, you should aim to understand the definition of solubility and the solubility product constant (Kₛₚ), including how to calculate and interpret Ksp values. You should learn to write and balance dissociation equations for sparingly soluble salts, apply the common ion effect, and perform calculations to determine the solubility of compounds in various conditions. Additionally, you should be able to explain selective precipitation and its applications, and understand the factors affecting solubility, such as pH and the presence of complex ions. These skills will enable you to solve related equilibrium problems and predict the behavior of ionic compounds in solution
Introduction
Solubility equilibria is a fundamental concept in chemistry that describes the dynamic balance between the dissolved ions and undissolved solid in a saturated solution. This equilibrium state is crucial in understanding how substances dissolve and precipitate under various conditions. It involves the solubility product constant (Kₛₚ), which quantifies the maximum amount of a solute that can dissolve in a solvent at a given temperature. Mastery of solubility equilibria principles is essential for predicting the behavior of salts in solutions, influencing various fields such as environmental chemistry, pharmacology, and industrial processes.
What is Solubility Equilibria?

Solubility equilibria refer to the dynamic balance between the dissolution and precipitation of a solute in a solvent, where the rate at which the solute dissolves equals the rate at which it precipitates out of solution, resulting in a constant concentration of dissolved ions at a given temperature and pressure. This equilibrium is described by the solubility product constant (Kₛₚ), which quantifies the maximum product of the molar concentrations of the constituent ions in a saturated solution.
Solubility Product Constant (Kₛₚ)
Kₛₚ is defined as the product of the molar concentrations of the constituent ions, each raised to the power of their respective coefficients in the balanced dissolution equation.
Dissolution Equation
Consider a general sparingly soluble salt AB, which dissociates in water as follows:
AB (s) ⇌ A⁺(aq) + B⁻(aq)
For this equilibrium, the solubility product expression (Kₛₚ) is:
Kₛₚ = [A⁺][B⁻]
Where:
- [A⁺] is the molar concentration of the cation.
- [B⁻] is the molar concentration of the anion.
Saturated Solution
A saturated solution is a chemical solution that contains the maximum concentration of a solute dissolved in a solvent at a specific temperature and pressure. In a saturated solution, the rate at which the solute dissolves equals the rate at which it precipitates out, resulting in a dynamic equilibrium.
Key Characteristics
- Maximum Solubility: The solute concentration is at its highest possible level without precipitating. Any additional solute added to the solution will not dissolve and will remain as a solid precipitate.
- Dynamic Equilibrium: The dissolution and precipitation of the solute occur at equal rates, meaning that the amount of dissolved solute stays constant over time, even though individual solute particles continue to dissolve and precipitate.
- Temperature and Pressure Dependent: The solubility of a solute in a solvent varies with temperature and pressure. A solution that is saturated at one temperature may become unsaturated if the temperature is increased or decreased.
Common Ion Effect
The common ion effect describes the phenomenon where the solubility of a sparingly soluble salt is reduced when a solution already contains one of the ions present in the salt. This effect is a consequence of Le Chatelier’s Principle, which states that the equilibrium of a system will shift to counteract a disturbance.
Key Characteristics
- Reduction in Solubility: The presence of a common ion decreases the solubility of the salt in solution.
- Shift in Equilibrium: The addition of a common ion shifts the dissolution equilibrium toward the formation of the undissolved solid, thereby reducing the concentration of dissolved ions.
- Application of Le Chatelier’s Principle: The system adjusts to maintain equilibrium by favoring the reverse reaction (precipitation) to reduce the disturbance caused by the added common ion.
Precipitation
Precipitation in chemistry refers to the process where dissolved ions in a solution combine to form an insoluble solid, known as a precipitate. This occurs when the concentration of the product of the ionic concentrations exceeds the solubility product constant (Kₛₚ) for a given compound.
Key Characteristics
- Formation of Insoluble Solid: Precipitation results in the formation of a solid from a solution when the ionic product exceeds the Ksp of the solute.
- Supersaturation: Precipitation typically occurs in a supersaturated solution where the concentration of dissolved ions exceeds their solubility.
- Dynamic Equilibrium: In a saturated solution, the rate of dissolution of the solid equals the rate of precipitation, maintaining a dynamic equilibrium.
- Factors Affecting Precipitation: Factors such as temperature, concentration of ions, and the presence of common ions or complexing agents can affect the precipitation process.
Steps to Calculate Solubility from Kₛₚ

- Write the Dissociation Equation : Identify the chemical formula of the salt and write the balanced equation for its dissociation into ions in water.
- Set Up the Kₛₚ Expression: Write the solubility product expression based on the dissociation equation. The Kₛₚ expression is the product of the molar concentrations of the ions, each raised to the power of their coefficients in the balanced equation.
- Express Ion Concentrations in Terms of Solubility (s): Assume the solubility of the salt is s mol/L. Express the concentration of each ion in terms of sss.
- Substitute and Solve for s: Substitute the concentrations expressed in terms of sss into the Kₛₚ expression and solve for s.
Examples
Example 1: Solubility of Silver Chloride (AgCl)
Given: Kₛₚ= 1.77 x 10⁻¹⁰
- Write the Dissociation Equation:
AgCl (s) ⇌ Ag⁺(aq) + Cl⁻(aq) - Set Up the Kₛₚ Expression:
Kₛₚ = [Ag⁺][Cl⁻] - Express Ion Concentrations in Terms of Solubility (s):
[Ag⁺]=s , [Cl⁻]s - Substitute and Solve for s:
Kₛₚ = s⋅s
1.77×10⁻¹⁰ = s2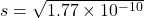
s ≈ 1.33 × 10⁻⁵M
The solubility of AgCl in water is approximately 1.33 × 10⁻⁵ M.
Example 2: Solubility of Calcium Phosphate (Ca₃(PO₄)₂)
Given: Kₛₚ = 2.07 × 10⁻³³
- Write the Dissociation Equation:
Ca₃(PO₄)₂(s) ⇌ 3Ca²⁺(aq) + 2PO₄³⁻(aq) - Set Up the Kₛₚ Expression:
Kₛₚ = [Ca²⁺]³[PO₄³⁻]² - Express Ion Concentrations in Terms of Solubility (s):
[Ca²⁺]= 3s
[PO₄³⁻] = 2s - Substitute and Solve for s:
Ksp = (3s)³(2s)²
Ksp = 27s³ ⋅ 4s²
Ksp = 108s⁵
2.07 × 10⁻³³ = 108s⁵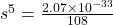
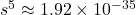
![Rendered by QuickLaTeX.com s \approx \sqrt[5]{1.92 \times 10^{-35}}](https://www.examples.com/wp-content/ql-cache/quicklatex.com-469dca24448edb14157d19cae24d2ec7_l3.png)
s ≈ 1.26×10⁻⁷ M
The solubility of Ca₃(PO₄)₂ in water is approximately 1.26×10⁻⁷ M.


