Introduction to Equilibrium

Learning Objectives

In the topic of Introduction to Equilibrium for the AP Chemistry exam, you should focus on understanding the dynamic nature of chemical equilibrium, the conditions necessary for equilibrium to occur, and the significance of the equilibrium constant (K) in different forms such as ( K꜀ ) and ( Kₚ ). You should learn to apply Le Chatelier’s Principle to predict the effects of changes in concentration, pressure, volume, and temperature on a system at equilibrium. Additionally, mastering the use of ICE tables to calculate equilibrium concentrations and recognizing the impact of catalysts on equilibrium will be crucial.

Introduction

Equilibrium is a fundamental concept in chemistry that describes the state of a system where the concentrations of reactants and products remain constant over time. This balance occurs when the rates of the forward and reverse reactions are equal, resulting in no net change in the amounts of substances involved. Understanding equilibrium is crucial for studying chemical reactions, as it helps predict how systems respond to changes in concentration, temperature, and pressure. This concept is pivotal in various fields, including industrial processes, environmental science, and biochemistry, making it essential for anyone studying or working in the field of chemistry.

What is Equilibrium?

Equilibrium in chemistry is the state in which the rate of the forward reaction equals the rate of the reverse reaction, resulting in the constant concentrations of reactants and products over time in a closed system.

Characteristics of Chemical Equilibrium

1. Dynamic Nature: At equilibrium, both the forward and reverse reactions continue to occur, but their rates are equal, so there is no net change in the concentrations of reactants and products.
2. Constant Concentrations: The concentrations of reactants and products remain constant over time once equilibrium is established, although they are not necessarily equal.
3. Closed System: Equilibrium can only be achieved in a closed system where no substances can enter or leave the system, ensuring that the amounts of reactants and products are conserved.
4. Reversible Reactions: Equilibrium occurs in reversible reactions where reactants convert to products and products convert back to reactants.
5. No Macroscopic Changes: At equilibrium, there are no observable changes in the properties of the system, such as color, pressure, or concentration, even though microscopic changes continue to happen.
6. Dependence on Temperature: The position of equilibrium and the equilibrium constant ((K)) are dependent on temperature, meaning that changes in temperature can shift the equilibrium position.
7. Independent of Initial Conditions: The final equilibrium state of a reaction is independent of the initial concentrations of reactants and products, although the time taken to reach equilibrium may vary.

The Equilibrium Constant (K)

The equilibrium constant (K) quantifies the ratio of the concentrations of products to reactants at equilibrium for a given reversible chemical reaction. It provides insight into the position of equilibrium and the extent to which a reaction proceeds.

Expression of the Equilibrium Constant

For a general reaction:

aA + bB ↔ cC + dD

The equilibrium constant in terms of concentration (K꜀) is expressed as:

\(K_c = \frac{[C]^c [D]^d}{[A]^a [B]^b}\)

• [A], [B], [C], [D] are the molar concentrations of the reactants (A, B) and products (C, D) at equilibrium.
• a, b, c, d are the stoichiometric coefficients from the balanced chemical equation.

Types of Equilibrium Constants

1. ( K꜀ ): Equilibrium constant expressed in terms of molar concentrations of reactants and products.
   \(K_c = \frac{[C]^c[D]^d}{[A]^a[B]^b}\)
2. ( Kₚ ): Equilibrium constant expressed in terms of partial pressures of gaseous reactants and products.
   \(K_p = \frac{(P_C)^c (P_D)^d}{(P_A)^a (P_B)^b}\)
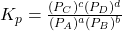
3. ( Kₛₚ ): Solubility product constant, used for sparingly soluble salts, indicating the product of the molar concentrations of the ions each raised to the power of their stoichiometric coefficients.
   \(K_{sp} = [\text{cation}]^m [\text{anion}]^n\)
4. ( Kₐ ): Acid dissociation constant, used for weak acids, indicating the extent of ionization of the acid in water.
   \(K_a = \frac{[H^+][A^-]}{[HA]}\)
5. ( K_b ): Base dissociation constant, used for weak bases, indicating the extent of ionization of the base in water.
   \(K_b = \frac{[BH^+][OH^-]}{[B]}\)
6. ( K_w ): Ion product constant for water, representing the product of the molar concentrations of hydrogen and hydroxide ions in water.
   \(K_w = [H^+][OH^-] = 1.0 \times 10^{-14} \, \text{at 25°C}\)

Le Chatelier’s Principle

Le Chatelier’s Principle states that if a system at equilibrium is disturbed by changing the conditions, the system will adjust to counteract the disturbance and restore a new equilibrium.

Applications of Le Chatelier’s Principle

1. Change in Concentration:
   • Adding Reactants: Shifts equilibrium towards products.
   • Removing Reactants: Shifts equilibrium towards reactants.
   • Adding Products: Shifts equilibrium towards reactants.
   • Removing Products: Shifts equilibrium towards products.
2. Change in Pressure and Volume (for gaseous reactions):
   • Increasing Pressure: Shifts equilibrium towards the side with fewer moles of gas.
   • Decreasing Pressure: Shifts equilibrium towards the side with more moles of gas.
3. Change in Temperature:
   • Exothermic Reactions: Increasing temperature shifts equilibrium towards reactants; decreasing temperature shifts it towards products.
   • Endothermic Reactions: Increasing temperature shifts equilibrium towards products; decreasing temperature shifts it towards reactants.
4. Addition of a Catalyst:
   • Does not affect the position of equilibrium but helps the system reach equilibrium faster.

Example

For the reaction ( N₂ (g) + 3H₂ (g) ↔ 2NH₃ (g) ) (exothermic):

• Increasing ( [N₂] ) or ( [H₂] ): Shifts equilibrium towards the formation of ( NH₃ ).
• Increasing Pressure: Shifts equilibrium towards ( NH₃ ) (fewer moles of gas).
• Increasing Temperature: Shifts equilibrium towards reactants (since the reaction is exothermic).

Calculating Equilibrium Concentrations

1. Write the Balanced Equation: Identify the balanced chemical equation for the reaction.
   • Description: This step provides the stoichiometric relationships needed for setting up the equilibrium expression.
2. Set Up an ICE Table: Use an ICE (Initial, Change, Equilibrium) table to track the concentrations of reactants and products.
   • Description: An ICE table helps organize initial concentrations, the changes that occur as the reaction proceeds to equilibrium, and the final equilibrium concentrations.
3. Express the Equilibrium Constant: Write the expression for the equilibrium constant (K꜀).
   • Description: This involves writing the ratio of the concentrations of the products to the reactants, each raised to the power of their coefficients in the balanced equation.
4. Determine Initial Concentrations: Insert the initial concentrations of the reactants and products into the ICE table.
   • Description: This step sets the starting point for calculating how concentrations change as the reaction moves towards equilibrium.
5. Define Changes in Concentrations: Determine the changes in concentrations of reactants and products using a variable.
   • Description: Assume that the concentration of reactants decreases by x and the concentration of products increases by an amount consistent with the stoichiometry of the reaction.
6. Calculate Equilibrium Concentrations: Apply the changes to the initial concentrations to find the equilibrium concentrations.
   • Description: Subtract the changes from the initial concentrations for reactants and add the changes to the initial concentrations for products.
7. Solve for the Unknowns: Use the equilibrium constant expression to solve for the variable (x) and the equilibrium concentrations.
   • Description: Substitute the equilibrium concentrations into the equilibrium expression and solve for x, then calculate the final concentrations of all species at equilibrium.

Factors Affecting Equilibrium

1. Concentration: Changing the concentration of reactants or products shifts the equilibrium to oppose the change.
2. Pressure/Volume: For gaseous reactions, increasing pressure (or decreasing volume) shifts the equilibrium towards the side with fewer gas molecules, while decreasing pressure (or increasing volume) shifts it towards the side with more gas molecules.
3. Temperature: Increasing temperature shifts the equilibrium in the direction of the endothermic reaction, while decreasing temperature shifts it towards the exothermic reaction.
4. Catalysts: Catalysts speed up the rate at which equilibrium is reached but do not change the position of the equilibrium.

Practice Problems

1. For the reaction 2NO₂(g) ↔ N₂O₄​(g), Kc=0.36 at 100°C. If the initial concentrations are [NO₂​]=0.50M and [N₂O₄​]=0.10 M, calculate the equilibrium concentrations of NO₂​ and N₂O₄​.

Solution:

Write the balanced equation:
2NO₂(g) ↔ N₂O₄​(g)

Set up the ICE table:

	NO₂(g)	N₂O₄​(g)
Initial (I)	0.50 M	0.10 M
Change (C)	-2x	+x
Equilibrium (E)	0.50 – 2x	0.10 + x

Write the equilibrium expression:
\(K_c = \frac{[N_2O_4]}{[NO_2]^2}\)

Substitute the equilibrium concentrations into the expression:
\(0.36 = \frac{0.10 + x}{(0.50 – 2x)^2}\)

Solve for ( x ):

• Expanding and simplifying the equation, we arrive at:\(1.44x^2 – 1.36x – 0.01 = 0\)
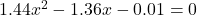
• Using the quadratic formula:\(x = \frac{1.36 \pm \sqrt{1.8496}}{2.88}\)
  \(x \approx 0.093 \, \text{M} \quad (\text{physically meaningful solution})\)

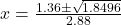
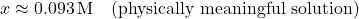
Calculate Equilibrium Concentrations:

• For \(NO(_2)\):\([\text{NO}_2] = 0.50 – 2(0.093) = 0.314, \text{M}\)
• For \(N(_2)O(_4):[\text{N}_2\text{O}_4] = 0.10 + 0.093 = 0.193 \, \text{M}]\)

[NO₂​] = 0.50 − 2(0.093) = 0.314M

[N₂O₄​] = 0.10 + 0.093 = 0.193M

2. Given the reaction N₂​(g) + 3H₂​(g) ↔ 2NH₃​(g), Kp=4.34×10⁻³ at 400°C. If the initial partial pressures are PN₂=1.00atm, PH₂=3.00 atm, and PNH₃ = 0.50 atm, find the equilibrium partial pressures of all species.

Solution:

Write the balanced equation:
N₂​(g) + 3H₂​(g) ↔ 2NH₃​(g)

Set up the ICE table:

	N₂​ (g)	H₂(g)	NH₃3​ (g)
Initial (I)	1.00 atm	3.00 atm	0.50 atm
Change (C)	-x	-3x	+2x
Equilibrium (E)	1.00 – x	3.00 – 3x	0.50 + 2x

Write the equilibrium expression:
\(K_p = \frac{(P_{NH_3})^2}{(P_{N_2})(P_{H_2})^3}\)

Substitute the equilibrium partial pressures into the expression:
\(4.34 \times 10^{-3} = \frac{(0.50 + 2x)^2}{(1.00 – x)(3.00 – 3x)^3}\)

Solve for ( x ):

Use iterative method or solver tools due to the complexity of the cubic equation.

Approximate solution for simplicity (detailed steps would involve numerical methods).

Calculate equilibrium partial pressures:

\(P_{N_2} = 1.00 – x \\ P_{H_2} = 3.00 – 3x \\ P_{NH_3} = 0.50 + 2x\)