Learning Objectives
By studying the topic of Free Energy of Dissolution for the AP Chemistry exam, you should be able to understand and calculate the Gibbs free energy change (ΔG) associated with the dissolution process, recognize the factors that influence the spontaneity of dissolution, and differentiate between the enthalpy (ΔH) and entropy (ΔS) components of the dissolution process. You should also be able to apply the concepts to predict whether a given dissolution will occur spontaneously at a specific temperature, use real-world examples such as the dissolution of ionic compounds in water, and explain the thermodynamic principles governing these processes.
Introduction
Free energy of dissolution quantifies the spontaneity of a solute dissolving in a solvent, governed by the Gibbs free energy change (ΔG). This change combines the system’s enthalpy (ΔH) and entropy (ΔS). A negative ΔG indicates a spontaneous dissolution process, essential for predicting solubility and designing pharmaceuticals. Understanding this concept is crucial for applications involving solute-solvent interactions.
What is Free Energy of Dissolution?

Free energy of dissolution is the change in Gibbs free energy (ΔGdissolution) that occurs when a solute dissolves in a solvent. It quantifies the thermodynamic feasibility of the dissolution process, determining whether the process is spontaneous (ΔG<0), non-spontaneous (ΔG > 0), or at equilibrium (ΔG = 0).
Gibbs Free Energy (ΔG)

Gibbs free energy (ΔG) is a thermodynamic potential that measures the maximum amount of work that can be performed by a thermodynamic system at constant temperature and pressure. It is a crucial concept for predicting the spontaneity of chemical reactions and processes. The Gibbs free energy change for a process is given by the equation:
ΔG = ΔH − TΔS
where:
- ΔH is the change in enthalpy (heat content) of the system.
- T is the absolute temperature in Kelvin.
- ΔS is the change in entropy (disorder) of the system.
Spontaneity of Dissolution
The spontaneity of dissolution refers to whether a solute will dissolve in a solvent without the input of external energy. This is determined by the change in Gibbs free energy (ΔGdissolution) for the dissolution process.
- Spontaneous Dissolution: If ΔGdissolution < 0, the dissolution process is spontaneous.
- Non-Spontaneous Dissolution: If ΔGdissolution > 0, the dissolution process is non-spontaneous.
- Equilibrium: If ΔGdissolution = 0, the system is at equilibrium, and the dissolution process is neither spontaneous nor non-spontaneous.
Enthalpy of Solution (ΔHsolution)
Enthalpy of solution (ΔHsolution) is the total heat change that occurs when a solute dissolves in a solvent to form a solution. It is the sum of the energy changes involved in breaking the intermolecular forces within the solute and solvent, as well as the energy change when new interactions form between the solute and solvent molecules. The enthalpy of solution can be either positive (endothermic) or negative (exothermic) depending on the nature of the interactions.
Components of Enthalpy of Solution
- Lattice Energy (ΔHlattice):
- The energy required to break the ionic bonds in the solid solute. This process is always endothermic (positive ΔH) because energy is needed to overcome the electrostatic forces holding the ions together in the crystal lattice.
- Hydration Energy (ΔHhydration):
- The energy released when ions are surrounded by solvent molecules, usually water in aqueous solutions. This process is typically exothermic (negative ΔH) because new attractions are formed between the ions and the solvent molecules.
Calculation of Enthalpy of Solution
The enthalpy of solution can be expressed as:
ΔHsolution = ΔHlattice + ΔHhydration
Endothermic vs. Exothermic Dissolution
- Endothermic Dissolution: When ΔHsolution is positive, the dissolution process absorbs heat from the surroundings. This happens when the energy required to break the solute-solvent interactions is greater than the energy released during the solvation process.
- Exothermic Dissolution: When ΔHsolution is negative, the dissolution process releases heat to the surroundings. This occurs when the energy released during solvation is greater than the energy required to break the solute-solvent interactions.
Entropy of Solution (ΔSsolution)
Entropy of solution (ΔSsolution) is the change in entropy when a solute dissolves in a solvent to form a solution. Entropy (S) is a measure of the disorder or randomness in a system. When a solute dissolves, the overall disorder of the system typically changes, influencing the spontaneity of the dissolution process.
Key Points about Entropy of Solution
- Increase in Disorder:
- When a solid solute dissolves in a solvent, the solute particles spread out and become more randomly distributed, usually increasing the entropy of the system.
- For ionic compounds, the ions separate and disperse throughout the solvent, significantly increasing disorder.
- Factors Affecting ΔSsolution:
- Nature of Solute and Solvent: The degree of increase in entropy depends on the types of solute and solvent involved.
- Temperature: Higher temperatures generally increase the entropy of the solution because particles move more vigorously and spread out more.
Calculation of ΔSsolution
ΔSsolution can be determined by comparing the entropy of the solution to the entropy of the solute and solvent before mixing:
ΔSsolution = Ssolution − (Ssolute + Ssolvent)
Spontaneity and Entropy
- A positive ΔSsolution favors the spontaneity of the dissolution process because it contributes to a negative ΔGdissolution (since ΔG = ΔH − TΔS).
Steps to Calculate Free Energy of Dissolution

- Determine the Enthalpy of Solution (ΔHsolution):
- Identify the lattice energy (ΔHlattice), which is the energy required to break the bonds in the solid solute. This value is usually positive (endothermic).
- Identify the hydration (or solvation) energy (ΔHhydration), which is the energy released when the solute particles interact with the solvent molecules. This value is usually negative (exothermic).
- Calculate ΔHsolution: ΔHsolution = ΔHlattice + ΔHhydration
- Calculate the Entropy of Solution (ΔSsolution):
- Determine the entropy change associated with the dissolution process. This can often be found in tables or given in the problem statement.
- ΔSsolution is typically positive because the solute particles spread out and increase disorder in the solution.
- Compute the Gibbs Free Energy Change (ΔGdissolution):
- Use the Gibbs free energy equation to calculate ΔGdissolution = ΔHsolution − TΔSsolution
- Here, T is the absolute temperature in Kelvin.
Factors Affecting Free Energy of Dissolution
- Temperature (T): Higher temperatures can favor dissolution if ΔSsolution is positive, as TΔSsolution becomes larger.
- Nature of Solute and Solvent: The type of solute and solvent affects ΔHsolution and ΔSsolution; ionic compounds often dissolve spontaneously in polar solvents.
- Concentration: The initial concentration of solute and solvent can shift the equilibrium and affect ΔGdissolution.
- Pressure: Primarily affects gases; higher pressure increases solubility of gases in liquids, impacting ΔGdissolution.
- Intermolecular Forces: Stronger solute-solvent interactions (e.g., hydrogen bonding) can lower ΔHsolution, making dissolution more favorable.
Practice Problems
1. Dissolution of Potassium Nitrate (KNO₃) in Water
- Determine
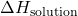 :
:
- Given:
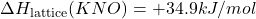
- Given:
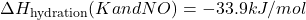
- Calculate
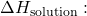
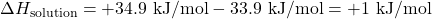
- Given:
- Calculate
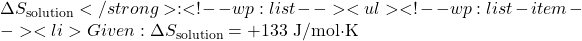
- Compute
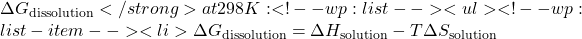

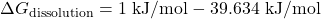
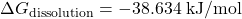
Since ![]() n is negative, the dissolution of KNO₃ in water is spontaneous at 298 K.
n is negative, the dissolution of KNO₃ in water is spontaneous at 298 K.
2: Dissolution of Ammonium Chloride (NH₄Cl) in Water
- Determine
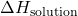 :
:
- Given:
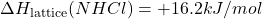
- Given:
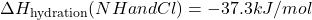
- Calculate
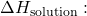
-
- Given:
- Calculate
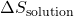 :
:
- Given:
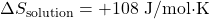
- Given:
- Compute
 at 298 K:
at 298 K:
-
Since ![]() is negative, the dissolution of NH₄Cl in water is spontaneous at 298 K.
is negative, the dissolution of NH₄Cl in water is spontaneous at 298 K.


