Introduction to Entropy

Last Updated: December 19, 2024

Notes

Learning Objectives

In the topic of Introduction to Entropy for the AP Chemistry exam, you should aim to understand and explain the concept of entropy as a measure of disorder or randomness in a system, comprehend the second law of thermodynamics and its implications for spontaneous processes, differentiate between microstates and macrostates, and use Boltzmann’s equation to relate entropy to the number of microstates. You should be able to calculate entropy changes (ΔS) for chemical reactions, phase changes, and temperature changes, and interpret these changes in the context of spontaneity and the Gibbs free energy equation (ΔG = ΔH − TΔS). Additionally, you should relate entropy changes to real-world processes such as melting, boiling, and dissolution, and understand the significance of the entropy of the universe (ΔS_universe) in predicting the spontaneity of processes.

Free AP Chemistry Practice Test

Introduction

Entropy is a fundamental concept in thermodynamics and statistical mechanics, often described as a measure of disorder or randomness in a system. It helps explain why certain processes occur naturally and why others do not. In essence, entropy quantifies the number of possible arrangements of particles in a system, with higher entropy indicating more possible configurations and greater disorder. Understanding entropy is crucial for studying the direction of spontaneous processes and the efficiency of energy conversion in physical and chemical systems.

What is Entropy?

Entropy is a thermodynamic quantity representing the unavailability of a system’s energy to do work, often interpreted as the degree of disorder or randomness in the system. It is symbolized by S and quantified in units of joules per kelvin (J/K). Entropy increases with the number of possible microstates of a system, reflecting the tendency of systems to move toward thermodynamic equilibrium and maximum disorder.

Key Concepts of Entropy

1. Spontaneity and Entropy

Spontaneous Processes: These are processes that occur without external intervention. A process is spontaneous if it leads to an increase in the entropy of the universe. For example, ice melting at room temperature is a spontaneous process because it leads to an increase in entropy.
Non-Spontaneous Processes: These require external energy input to occur and often result in a decrease in the system’s entropy. For example, compressing a gas into a smaller volume is non-spontaneous and requires work to be done on the system.

2. Microstates and Macrostates

Microstates: These are the specific detailed microscopic configurations of a system. Each microstate represents a possible arrangement of the particles in a system.
Macrostates: These are the overall states of a system, defined by macroscopic properties such as temperature, pressure, and volume. A macrostate can correspond to many different microstates.
Boltzmann’s Equation: This equation, S = 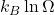$k_B \ln \Omega$ , relates the entropy (S) of a system to the number of possible microstates (Ω). Here, k_B is Boltzmann’s constant. This equation highlights that as the number of microstates increases, the entropy of the system also increases.

3. Second Law of Thermodynamics

Statement: The second law of thermodynamics states that the total entropy of an isolated system can never decrease over time. It can either increase or remain constant.
Implication: This law implies that natural processes tend to move toward a state of maximum entropy. For example, heat will spontaneously flow from a hot object to a cold one until thermal equilibrium is reached, maximizing the entropy.

Measuring Entropy

1. Standard Molar Entropies

Standard molar entropy (S^∘) is the entropy content of one mole of a substance under standard conditions (298 K, 1 atm pressure). These values are usually tabulated and can be found in chemistry reference materials.

Units: Joules per mole per Kelvin (J/mol·K).
Significance: Standard molar entropy values allow chemists to compare the disorder of different substances under identical conditions.

2. Entropy Changes in Chemical Reactions

To understand how a chemical reaction affects the entropy of a system, we calculate the entropy change (ΔS) for the reaction.

Formula:

ΔS_reaction = ∑S_products^∘ − ∑S_reactants

∑S_products^∘: The sum of the standard molar entropies of all the products.
∑S_reactants∘: The sum of the standard molar entropies of all the reactants.

3. Calculating Entropy Change

For Phase Changes

Entropy changes significantly during phase transitions due to changes in molecular order and freedom of movement.

Melting (Fusion):
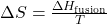
- ΔH_fusion: Enthalpy of fusion (heat required to melt the substance).
- T: Temperature at which the phase change occurs.
Boiling (Vaporization):
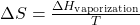
- ΔH_vaporization: Enthalpy of vaporization (heat required to vaporize the substance).
- T: Temperature at which the phase change occurs.

For Temperature Changes

Entropy changes can also be calculated for processes where the temperature of a substance changes without a phase change.

$\Delta S = nC_p \ln \left( \frac{T_2}{T_1} \right)$

n: Number of moles of the substance.
C_p: Molar heat capacity at constant pressure.
T₁: Initial temperature.
T₂: Final temperature.

4. Third Law of Thermodynamics

The third law of thermodynamics states that the entropy of a perfect crystal at absolute zero (0 K) is zero. This provides a reference point for measuring absolute entropies.

Entropy and the Universe

1. Entropy of the Universe

The second law of thermodynamics states that the total entropy of the universe always increases for any spontaneous process. This law highlights the natural tendency towards disorder and energy dispersion.

Formula:

ΔS_universe = ΔS_system + ΔS_surroundings

ΔS_universe: Change in the entropy of the universe.
ΔS_system: Change in the entropy of the system.
ΔS_surroundings: Change in the entropy of the surroundings.

For a process to be spontaneous, ΔS_universe must be greater than zero. This means that the increase in entropy of the surroundings must compensate for any decrease in the entropy of the system, leading to a net increase in the universe’s total entropy.

2. Gibbs Free Energy and Entropy

Gibbs free energy (G) is a thermodynamic potential that can predict the spontaneity of a process. The relationship between Gibbs free energy, enthalpy, and entropy is given by:

ΔG = ΔH − T

ΔG Change in Gibbs free energy.
ΔH: Change in enthalpy (heat content) of the system.
T: Absolute temperature in Kelvin.
ΔS: Change in entropy of the system.

Conditions for Spontaneity:

ΔG < 0: The process is spontaneous.
ΔG = 0: The system is in equilibrium.
ΔG > 0: The process is non-spontaneous.

3. Heat Exchange and Entropy

The change in entropy of the surroundings is often related to the heat exchange between the system and the surroundings.

Formula:

$\Delta S_{\text{surroundings}} = -\frac{q_{\text{system}}}{T}$

q_system: Heat absorbed or released by the system.
T: Absolute temperature in Kelvin.

A process that releases heat (q_system < 0) increases the entropy of the surroundings, while a process that absorbs heat (q_system > 0) decreases the entropy of the surroundings.

4. Entropy and the Arrow of Time

Entropy is often associated with the arrow of time. The increase in entropy provides a direction to time, indicating that time naturally progresses in the direction in which entropy increases. This concept explains why certain processes, like the mixing of gases or the melting of ice, occur naturally in one direction but not in the reverse direction.

5. Examples in Nature

Ice Melting: When ice melts to form water, the system’s entropy increases as the rigid structure of ice breaks down into the more disordered liquid state. The heat absorbed from the surroundings decreases the surroundings’ entropy, but the overall entropy of the universe increases.
Combustion: During combustion, complex fuel molecules break down into simpler molecules like CO₂ and H₂O, increasing the system’s entropy. The heat released increases the entropy of the surroundings, ensuring a positive ΔS_universe.
Biological Processes: In living organisms, local decreases in entropy (like the formation of ordered structures) are compensated by increases in the entropy of the surroundings, ensuring that the total entropy of the universe increases.