Reaction Rate

Learning Objectives

By the end of this topic, you should be able to define reaction rate, explain factors affecting reaction rate, describe methods of measuring reaction rate, formulate and determine rate laws, and understand reaction mechanisms for AP Chemistry.

Introduction

The reaction rate is a measure of how quickly a chemical reaction occurs. It quantifies the change in concentration of reactants or products per unit time. Several factors influence the reaction rate, including temperature, concentration of reactants, surface area, and the presence of catalysts. Understanding reaction rates is crucial in fields such as chemical engineering, pharmacology, and environmental science, as it helps in optimizing conditions for desired reactions and in controlling the rates of unwanted or hazardous reactions

What is Reaction Rate?

Reaction rate is the speed at which reactants are converted into products in a chemical reaction, typically measured as the change in concentration of a reactant or product per unit time.

Formula for Reaction Rate

\text{Rate} = \frac{\Delta [\text{Reactant}]}{\Delta t}

\text{Rate} = \frac{\Delta [\text{Product}]}{\Delta t}

where Δ[Reactant] or Δ[Product] is the change in concentration of the reactant or product over the time interval Δt.

Factors Affecting Reaction Rate

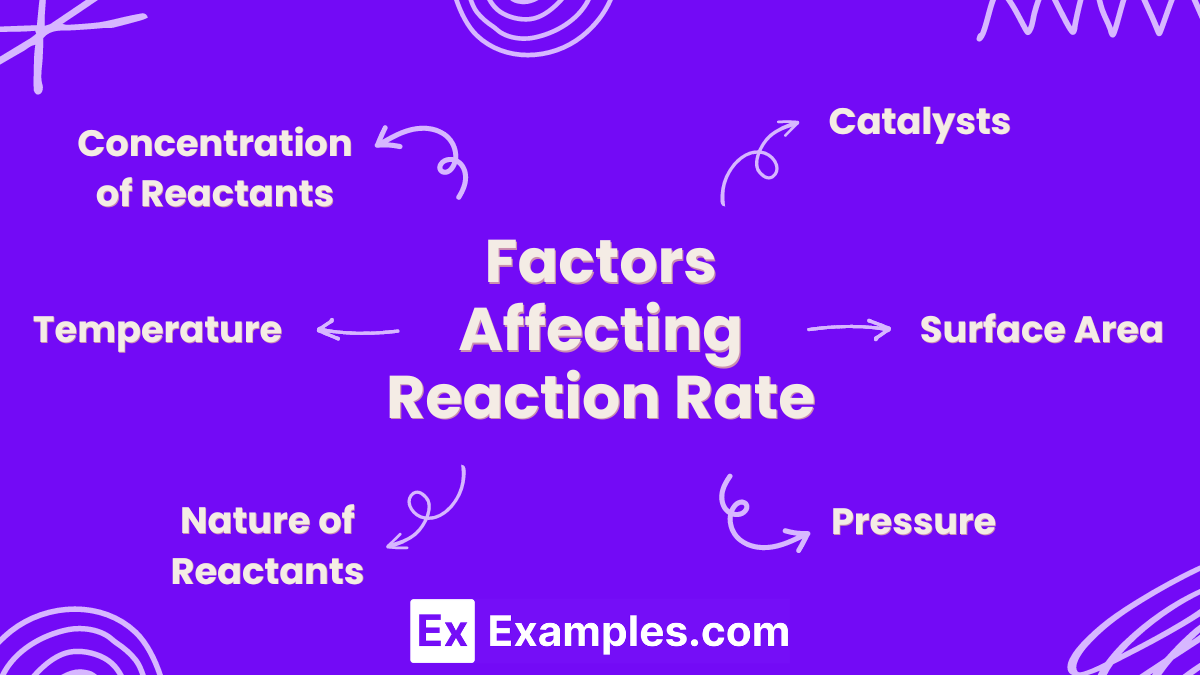
1. Concentration of Reactants

Higher Concentration: Increases the frequency of collisions between reactant molecules, leading to an increased reaction rate.
Lower Concentration: Decreases the frequency of collisions, leading to a decreased reaction rate.

2. Temperature

Higher Temperature: Increases the kinetic energy of molecules, resulting in more frequent and energetic collisions, which increases the reaction rate.
Lower Temperature: Decreases the kinetic energy of molecules, leading to fewer and less energetic collisions, which decreases the reaction rate.

3. Surface Area

Larger Surface Area: For solid reactants, increasing the surface area allows more collisions to occur, thus increasing the reaction rate.
Smaller Surface Area: Reduces the area available for collisions, thereby decreasing the reaction rate.

4. Catalysts

Presence of Catalysts: Catalysts lower the activation energy required for the reaction, increasing the rate without being consumed in the process.
Absence of Catalysts: Higher activation energy is needed, which slows down the reaction rate.

5. Nature of Reactants

Chemical Nature: Different substances react at different rates depending on their chemical nature and bond structures. For example, ionic compounds typically react faster than covalent compounds.
Bond Strength: Weaker bonds generally result in faster reactions, while stronger bonds slow down the reaction rate.

6. Pressure

Increased Pressure: For reactions involving gases, increasing the pressure forces molecules closer together, increasing the frequency of collisions and the reaction rate.
Decreased Pressure: Reduces the frequency of collisions among gas molecules, thereby decreasing the reaction rate.

Methods to Measure Reaction Rate

Volume of Gas Produced: Measures the volume of gas evolved in reactions involving gaseous products. This method involves capturing and measuring the gas produced over time to determine the rate of reaction.
Change in Mass: Observes the mass change in reactions where a gas is produced or consumed. By measuring the decrease in mass as gas escapes or the increase in mass as gas is absorbed, the reaction rate can be calculated.
Color Change: Uses a colorimeter to track color changes in reactions involving colored substances. By measuring the intensity of the color at regular intervals, the concentration of reactants or products can be determined, indicating the reaction rate.
Change in pH: Monitors pH changes in reactions producing or consuming hydrogen ions. Using a pH meter or pH indicators, the change in acidity or alkalinity of the solution is measured, which correlates to the reaction rate.
Titration: Involves periodically removing samples from the reaction mixture and titrating to determine the concentration of a reactant or product. This method provides precise measurements of concentration changes over time.
Conductivity: Measures the change in electrical conductivity of a solution as the reaction progresses. As the concentration of ionic species changes during the reaction, the conductivity of the solution will vary, providing information on the reaction rate.
Spectroscopy: Uses spectroscopic techniques to measure the concentration of reactants or products based on their interaction with light. Techniques such as UV-Vis spectroscopy monitor the absorbance or emission of light, which changes as the reaction proceeds.
Pressure Change: Measures the change in pressure in a closed system for reactions involving gases. By monitoring the pressure inside a reaction vessel, the rate at which gaseous reactants are consumed or gaseous products are formed can be determined.

Rate Laws

Rate laws describe the relationship between the rate of a chemical reaction and the concentration of its reactants. The rate law for a reaction is determined experimentally and can provide insights into the reaction mechanism.

General Form of Rate Law

The general form of a rate law is expressed as:

\text{Rate} = k [A]^m [B]^n

where:

Rate is the rate of the reaction.
k is the rate constant.
[A] and [B] are the concentrations of reactants A and B.
m and n are the reaction orders with respect to reactants A and B, respectively.

Reaction Orders

Reaction orders (m and n) indicate how the rate of reaction is affected by the concentration of each reactant:

Zero-Order Reaction: The rate is independent of the concentration of the reactant. \text{Rate} = k
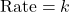
First-Order Reaction: The rate is directly proportional to the concentration of the reactant. \text{Rate} = k[A]
Second-Order Reaction: The rate is proportional to the square of the concentration of the reactant. \text{Rate} = k[A]^2
Mixed-Order Reaction: The rate depends on the concentration of multiple reactants, each with its own order. For example, \text{Rate} = k[A]^m[B]^n

Determining Rate Laws

Rate laws are determined experimentally by measuring reaction rates at different concentrations of reactants. Two common methods include:

Initial Rates Method:
- Measure the initial rate of reaction for different initial concentrations of reactants.
- Use the data to determine the reaction order with respect to each reactant.
Integrated Rate Laws:
- Use concentration vs. time data to determine the rate law and reaction order.
- For a first-order reaction: [ [A]_t = [A]_0 e^{-kt} ]
- For a second-order reaction: [ \frac{1}{[A]_t} = \frac{1}{[A]_0} + kt ]

Rate Constant (k)

The rate constant (kkk) is a proportionality constant that is specific to a given reaction at a given temperature. It can be determined experimentally and its units vary depending on the overall order of the reaction:

Zero-Order: \text{units of } k = \text{M} \cdot \text{s}^{-1}
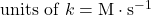
First-Order: \text{units of } k = \text{s}^{-1}
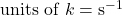
Second-Order: \text{units of } k = \text{M}^{-1} \cdot \text{s}^{-1}

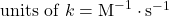
Example Problem

Consider the reaction:

2NO₂ (g) → 2NO(g) + O₂(g)

The following data were collected at a constant temperature:

Experiment	[NO₂] (M)	Initial Rate (M/s)
1	0.010	0.020
2	0.020	0.080
3	0.030	0.180

Determine the rate law, the rate constant k, and the order of the reaction with respect to NO₂.

Solution:

Determine the Reaction Order:

From the data, observe how the initial rate changes with the concentration of NO2NO_2NO2.

Comparing experiments 1 and 2:
- When [NO₂] doubles from 0.010 M to 0.020 M, the rate increases from 0.020 M/s to 0.080 M/s.
- Rate increase factor: 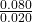\frac{0.080}{0.020} = 4
- Concentration increase factor: 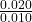\frac{0.020}{0.010} = 2

Since (2n=4)(2^n = 4)(2n=4), n=2n = 2n=2.

Comparing experiments 2 and 3:
- When [NO₂] increases from 0.020 M to 0.030 M, the rate increases from 0.080 M/s to 0.180 M/s.
- Rate increase factor: 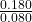\frac{0.180}{0.080} = 2.25
- Concentration increase factor: 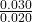\frac{0.030}{0.020} = 1.5

Since (1.5² = 2.25), this confirms that the reaction is second-order with respect to NO₂.

Write the Rate Law:

Given that the reaction is second-order with respect to NO₂:

\text{Rate} = k [NO_2]^2

Calculate the Rate Constant kkk:

Using the data from any experiment, substitute the values into the rate law to solve for k.

From Experiment 1:

0.020M/s = k(0.010M)²

0.020M/s = k(0.0001M²)

k = \frac{0.020 \, \text{M/s}}{0.0001 \, \text{M}^2}

k=200M⁻¹ s⁻¹