Learning Objectives
By the end of this lesson, you should be able to balance chemical equations to ensure the law of conservation of mass is upheld, determine molar ratios from balanced chemical equations to relate amounts of reactants and products, identify the limiting reactant in a chemical reaction to predict the amount of products formed, calculate theoretical yields of products based on stoichiometric relationships, compute percent yield from actual and theoretical yields to evaluate reaction efficiency, perform conversions between moles, mass, and volume using molar masses and the ideal gas law, derive empirical and molecular formulas from percent composition and molar mass data, and apply stoichiometric principles to solve real-world problems and laboratory scenarios, all of which are essential skills for success in AP Chemistry.
Introduction
Stoichiometry is the branch of chemistry that focuses on the quantitative relationships between reactants and products in chemical reactions, allowing chemists to predict the amounts of substances consumed and produced. It involves using balanced chemical equations to determine molar ratios, identify limiting reactants, and calculate theoretical yields, enabling precise conversions between moles, mass, and volume, which are essential for both theoretical problem-solving and practical laboratory applications in AP Chemistry.
What is Stoichiometry?

Stoichiometry is the branch of chemistry that deals with the quantitative relationships between the amounts of reactants and products in a chemical reaction. It involves using balanced chemical equations to determine the ratios of reactants and products, allowing chemists to calculate the amounts of substances needed or produced in a given reaction.
Balancing Chemical Equations
Balancing chemical equations is a fundamental skill in stoichiometry that ensures the law of conservation of mass is upheld. In a balanced equation, the number of atoms of each element is the same on both sides of the equation. This is crucial for accurately determining the relationships between reactants and products.
Steps to Balance a Chemical Equation
- Write the Unbalanced Equation: Start by writing the skeletal equation with the correct chemical formulas of the reactants and products.
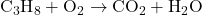
- Count the Atoms of Each Element: List the number of atoms of each element present in the reactants and products.
- Reactants: C = 3, H = 8, O = 2
- Products: C = 1, H = 2, O = 3
- Balance One Element at a Time: Adjust the coefficients (the numbers in front of the molecules) to balance the atoms of one element at a time. Start with elements that appear in only one reactant and one product.
- Balance Carbon (C):
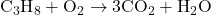
- Reactants: C = 3, H = 8, O = 2
- Products: C = 3, H = 2, O = 7
- Balance Hydrogen (H):
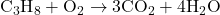
- Reactants: C = 3, H = 8, O = 2
- Products: C = 3, H = 8, O = 10
- Balance Carbon (C):
- Balance Oxygen (O): Since oxygen appears in both CO₂ and H₂O, adjust the coefficient of O₂ last.
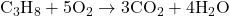
- Reactants: C = 3, H = 8, O = 10
- Products: C = 3, H = 8, O = 10
- Verify the Balance: Ensure that the number of atoms for each element is the same on both sides of the equation.
- Reactants: C = 3, H = 8, O = 10
- Products: C = 3, H = 8, O = 10
Molar Ratios
Molar ratios are the ratios of the coefficients of reactants and products in a balanced chemical equation, indicating the relative number of moles of each substance involved in the reaction.
Example of Molar Ratios
Consider the balanced chemical equation for the synthesis of ammonia (NH₃) from nitrogen (N₂) and hydrogen (H₂): \text{N}_2 + 3\text{H}_2 \rightarrow 2\text{NH}_3
From this equation, the molar ratios are:
- 1 mole of N₂ reacts with 3 moles of H₂
- 1 mole of N₂ produces 2 moles of NH₃
- 3 moles of H₂ produce 2 moles of NH₃
These ratios can be written as: ![]()
Using Molar Ratios in Calculations
Molar ratios allow chemists to calculate the amount of one substance based on the amount of another. This is useful for determining how much reactant is needed or how much product can be formed.
Example: How many moles of ammonia (NH₃) can be produced from 5 moles of hydrogen (H₂)?
- Write down the known information:
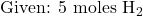
- Identify the relevant molar ratio from the balanced equation:
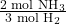
- Set up the conversion using the molar ratio:
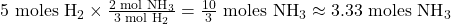
So, 5 moles of hydrogen can produce approximately 3.33 moles of ammonia.
Limiting Reactant
The limiting reactant is the reactant in a chemical reaction that is completely used up first, preventing any further reaction from occurring and thus limiting the amount of products formed.
Steps to Identify the Limiting Reactant
- Write the Balanced Chemical Equation: Ensure the chemical equation is balanced with the correct coefficients for each reactant and product.
- Convert All Given Reactant Quantities to Moles: Use molar masses to convert grams to moles, or use volume and molarity for solutions.
- Use Molar Ratios to Compare Amounts of Reactants: Based on the balanced equation, determine how many moles of each reactant are needed.
- Identify the Reactant That Produces the Least Amount of Product: This reactant is the limiting reactant.
Example
Consider the reaction between nitrogen (N₂) and hydrogen (H₂) to form ammonia (NH₃): ![]()
Problem: Determine the limiting reactant when 5 moles of N₂ react with 12 moles of H₂.
Solution:
- Write the balanced equation:
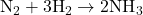
- Convert quantities to moles (if necessary): Given in moles already.
- Use molar ratios to determine the required moles:
- According to the balanced equation, 1 mole of N₂ requires 3 moles of H₂.
- For 5 moles of N₂: 5
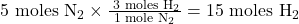
- Compare the actual moles to the required moles:
- You have 12 moles of H₂, but 15 moles are required to react with 5 moles of N₂.
- Therefore, H₂ is the limiting reactant.
Calculating Product Amounts
Once the limiting reactant is identified, you can calculate the amount of product formed.
Continuing the Example:
- Determine the amount of NH₃ produced:
- According to the balanced equation, 3 moles of H₂ produce 2 moles of NH₃.
- Therefore, 12 moles of H₂ will produce:
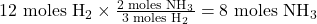
Theoretical Yield and Percent Yield
Theoretical Yield
Theoretical yield is the maximum amount of product that can be produced from a given amount of reactants, based on the stoichiometric calculations from a balanced chemical equation. It assumes perfect conditions where all reactants are fully converted to products without any losses.
Calculating Theoretical Yield
- Write the Balanced Chemical Equation: Ensure the equation is balanced with the correct coefficients for each reactant and product.
- Convert All Given Reactant Quantities to Moles: Use molar masses to convert grams to moles, or use volume and molarity for solutions.
- Use Molar Ratios to Calculate Moles of Product: Determine the number of moles of product that can be formed from the given moles of reactants using the balanced equation.
- Convert Moles of Product to Mass: Use the molar mass of the product to convert moles to grams, if necessary.
Example of Theoretical Yield Calculation
Consider the reaction between nitrogen (N₂) and hydrogen (H₂) to form ammonia (NH₃): ![]()
Problem: Calculate the theoretical yield of NH₃ when 10 grams of N₂ react with excess H₂.
- Write the balanced equation:
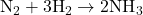
- Convert N₂ to moles:
- Molar mass of N₂ =
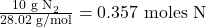
- Molar mass of N₂ =
- Use molar ratios to calculate moles of NH₃:
- 1 mole of N₂ produces 2 moles of NH₃.
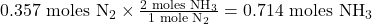
- 1 mole of N₂ produces 2 moles of NH₃.
- Convert moles of NH₃ to grams:
- Molar mass of NH₃ =
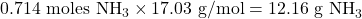
- Molar mass of NH₃ =
So, the theoretical yield of NH₃ is 12.16 grams.
Percent Yield

Percent yield is the ratio of the actual yield (the amount of product actually obtained from a reaction) to the theoretical yield, expressed as a percentage. It measures the efficiency of a reaction and indicates how much of the theoretical yield was actually produced.
![]()
Calculating Percent Yield
- Determine the Actual Yield: This is the amount of product actually obtained from the experiment.
- Calculate the Theoretical Yield: Use stoichiometric calculations to determine the theoretical yield, as shown above.
- Use the Percent Yield Formula: Plug the actual yield and theoretical yield into the percent yield formula.
Percent Yield=![]()
Example of Percent Yield Calculation
Problem: If the actual yield of NH₃ in the above example is 10 grams, what is the percent yield?
- Determine the actual yield:
- Actual yield = 10 grams
- Calculate the theoretical yield:
- Theoretical yield = 12.16 grams (from the previous example)
- Use the percent yield formula: Percent Yield=
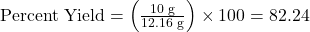
So, the percent yield is 82.24%.
Conversions Between Moles, Mass, and Volume

- Mole (mol): A unit representing 6.022 x 10²³ particles (atoms, molecules, or ions) of a substance.
- Mass: The quantity of matter in a substance, typically measured in grams (g) or kilograms (kg).
- Volume: The amount of space occupied by a substance, usually measured in liters (L) or milliliters (mL).
Key Relationships and Conversion Factors
- Moles to Mass:
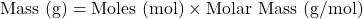
- Mass to Moles:
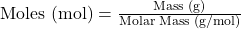
- Moles to Volume (for gases at STP – Standard Temperature and Pressure, 0°C and 1 atm):
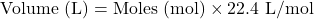
- Volume to Moles (for gases at STP):
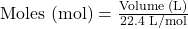
- Ideal Gas Law (for gases not at STP): PV=nRTPV = nRTPV=nRT
- P = pressure (atm)
- V = volume (L)
- n = moles (mol)
- R = ideal gas constant (0.0821 L·atm/mol·K)
- T = temperature (K)
Empirical and Molecular Formulas
Empirical Formula
The empirical formula of a compound is the simplest whole-number ratio of the elements present in the compound.
Determining the Empirical Formula
- Convert the Masses to Moles: If given percentages, assume a 100-gram sample, which converts the percentages directly to grams.
- Calculate the Moles of Each Element: Use the molar mass of each element.
- Divide by the Smallest Number of Moles: This gives the simplest whole-number ratio.
- Multiply to Obtain Whole Numbers: If necessary, multiply the ratios by an integer to get whole numbers.
Molecular Formula
The molecular formula of a compound is the actual number of atoms of each element in a molecule of the compound. It can be a multiple of the empirical formula.
Determining the Molecular Formula:
- Determine the Empirical Formula: Follow the steps above.
- Calculate the Empirical Formula Mass: Add up the atomic masses of the elements in the empirical formula.
- Divide the Molar Mass by the Empirical Formula Mass: This gives the multiplication factor.
- Multiply the Empirical Formula by the Factor: This gives the molecular formula.


