Ohms Law

What is Ohm’s Law?

Ohm’s Law states that the current flowing through a conductor between two points is directly proportional to the voltage across the two points and inversely proportional to the resistance between them.

Ohm’s Law Formula

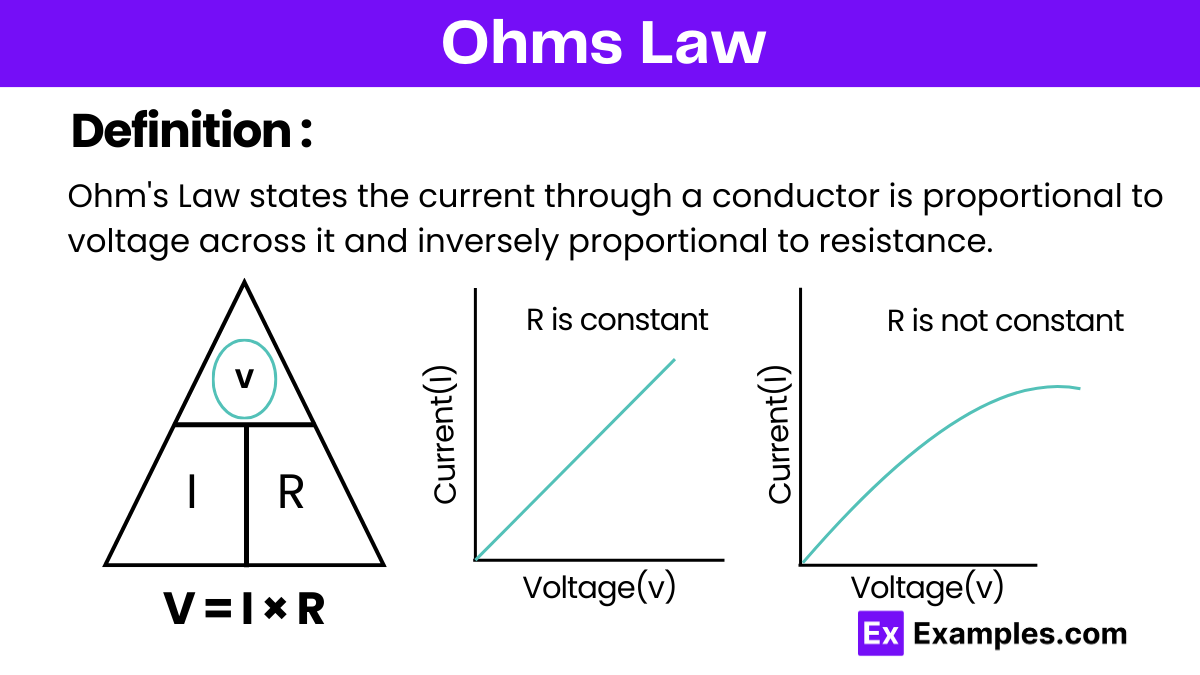
Ohm’s Law is fundamental in the study of electricity, and its formula is given by:

V = IR

Where:
V represents the voltage across the conductor (in volts, V)
I is the current flowing through the conductor (in amperes, A)
R denotes the resistance of the conductor (in ohms, Ω)

Relationship Between Voltage, Current and Resistance

Condition	Voltage (V)	Current (I)	Resistance (R)
Fixed Resistance	Increases	Increases	Constant
Fixed Current	Increases	Constant	Increases
Fixed Voltage	Constant	Decreases	Increases

Ohm’s Law Matrix Table

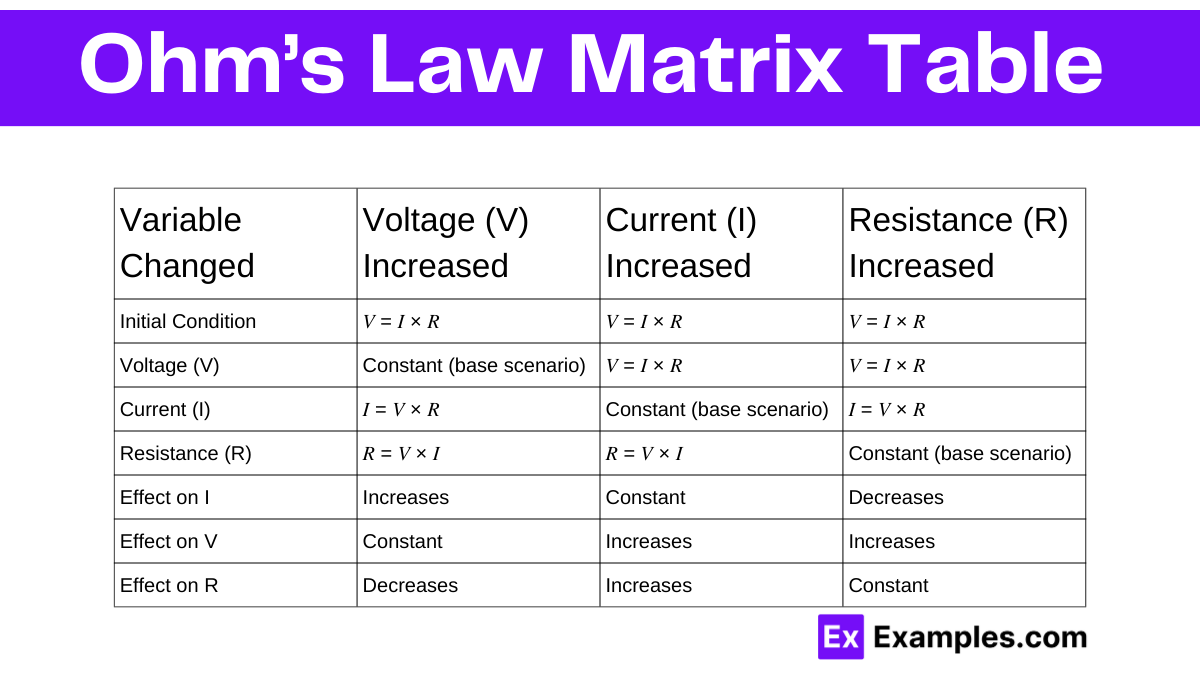
Variable Changed	Voltage (V) Increased	Current (I) Increased	Resistance (R) Increased
Initial Condition	𝑉 = 𝐼 × 𝑅	𝑉 = 𝐼 × 𝑅	𝑉 = 𝐼 × 𝑅
Voltage (V)	Constant (base scenario)	𝑉 = 𝐼 × 𝑅	𝑉 = 𝐼 × 𝑅
Current (I)	𝐼 = 𝑉 × 𝑅​	Constant (base scenario)	𝐼 = 𝑉 × 𝑅​
Resistance (R)	𝑅 = 𝑉 × 𝐼​	𝑅 = 𝑉 × 𝐼​	Constant (base scenario)
Effect on I	Increases	Constant	Decreases
Effect on V	Constant	Increases	Increases
Effect on R	Decreases	Increases	Constant

Table Explanation:

• Variable Changed: This column identifies which element of the equation is being manipulated or observed for change.
• Voltage (V) Increased: When voltage is increased while keeping resistance constant, current naturally increases. If resistance increases with constant current, voltage must also increase.
• Current (I) Increased: To increase current, either voltage must be increased (with constant resistance) or resistance must be decreased (with constant voltage).
• Resistance (R) Increased: Increasing resistance while maintaining constant current will result in an increase in voltage. Conversely, if the voltage is fixed, increasing resistance leads to a decrease in current.

Calculating Electrical Power Using Ohm’s Law

Electrical power, measured in watts, can be calculated using Ohm’s Law, which provides a direct way to find the power consumed by an electrical component when you know the voltage across it, the Current flowing through it, or the resistance it provides. There are several formulas derived from Ohm’s Law that make these calculations straightforward.

Basic Power Formula
The most basic formula for electrical power (P) in terms of voltage (V) and current (I) is:

P = V × I

Derived Formulas Using Ohm’s Law
Since
V=IR (Ohm’s Law), you can substitute in this relationship to find power in terms of either current and resistance, or voltage and resistance:

Power in terms of current and resistance:

P = I² × R

This formula is useful when you know the current and resistance but do not know the voltage. It shows that power increases with the square of the current, meaning even small increases in current can lead to large increases in power consumption if the resistance stays the same.
Power in terms of voltage and resistance:

P = V²/R

This is useful when you know the voltage and resistance. It illustrates that power increases with the square of the voltage, indicating that higher voltages can dramatically increase power consumption for the same resistance.

Ohm’s Law Pie Chart

Components of the Pie Chart:

1. Voltage (Volts, V)
   • Formula: 𝑉 = 𝐼 × 𝑅
   • Description: Voltage is the electrical potential difference and is the driving force that pushes the current through a circuit.
2. Current (Amperes, I)
   • Formula: 𝐼 = 𝑉 × 𝑅​
   • Description: Current is the rate of flow of electric charge. It’s determined by the voltage applied and the resistance of the circuit.
3. Resistance (Ohms, Ω)
   • Formula: 𝑅 = 𝑉 × 𝐼​
   • Description: Resistance is the property that opposes the flow of electric current. It determines how much current will flow for a given voltage.
4. Power (Watts, P)
   • Formula: 𝑃 = 𝑉 × 𝐼 or P = I²R or 𝑃 = 𝑉²/𝑅
   • Description: Power is the rate of doing work or the rate of using energy, which are equivalently expressed in watts in electrical terms.
5. Amplifier
   • Role in the Chart: An amplifier isn’t directly part of Ohm’s Law, but it relates to how voltage, current, and resistance interact in electronic circuits. Amplifiers use these elements to increase the power of a signal.

Applications of Ohm’s Law

1. Designing Electrical Circuits

Ohm’s Law is crucial for designing and analyzing electrical circuits. By knowing the voltage source and the resistance of the components, engineers can calculate the current that will flow through each part of the circuit. This helps in selecting appropriate components that can handle the expected current and voltage levels, ensuring safety and efficiency.

2. Electrical Measurements

Technicians use Ohm’s Law to determine unknown values in a circuit, such as identifying an unknown resistance by measuring the current flowing and the voltage across the resistor. This application is fundamental in troubleshooting and maintaining electrical systems.

3. Power Management

Ohm’s Law is used to calculate power consumption in electrical devices, which is vital for energy management and efficiency. Knowing how voltage, current, and resistance interact helps in optimizing power use and designing systems that are both energy-efficient and cost-effective.

4. Battery Life Calculations

For devices powered by batteries, Ohm’s Law helps predict battery life based on the current draw and the load’s resistance. This is essential for portable electronic devices such as smartphones, laptops, and medical equipment.

5. Heating Applications

The relationship given by 𝑃=𝐼2𝑅P=I2R indicates that power dissipation in a resistor (often used as a heating element) depends on the square of the current and the resistance. This principle is used in designing heating elements for appliances like electric heaters, toasters, and ovens.

6. Voltage Dividers

Ohm’s Law is employed in creating voltage dividers, where the voltage is divided among components in a series circuit proportional to their resistance. This technique is commonly used in signal processing and when working with sensors.

7. Automotive Applications

In automotive engineering, Ohm’s Law is used to ensure that electrical components such as lights, sensors, and motors receive the correct voltage and current. This is crucial for the reliability and functionality of modern vehicles.

8. Telecommunications

In the telecommunications industry, Ohm’s Law helps in the design and maintenance of networks, especially in determining the right settings for electrical signals passing through various resistive components in the network infrastructure.

9. Education and Training

Ohm’s Law is a foundational concept in education, providing a basis for students and trainees in fields related to electrical engineering and physics. It is one of the first principles taught to help students understand more complex electrical theories and applications.

Examples of Ohm’s Law

Calculating Current

Given:

• Voltage (V) = 12 volts
• Resistance (R) = 6 ohms

Find: Current (I)

Solution: Using the formula 𝐼=𝑉𝑅​, 𝐼=12 𝑉/6 Ω=2 𝐴

Result: The current flowing through the circuit is 2 amperes.

Determining Voltage

Given:

• Current (I) = 3 amperes
• Resistance (R) = 4 ohms

Find: Voltage (V)

Solution: Using 𝑉=𝐼𝑅, 𝑉=3 𝐴×4 Ω=12 𝑉

Result: The voltage across the circuit is 12 volts.

Frequently Asked Questions – FAQs

How do I calculate the resistance using Ohm’s Law?

To calculate the resistance in a circuit when you know the voltage and current, you can rearrange the formula: 𝑅=𝑉/𝐼​. For example, if the voltage is 10 volts and the current is 2 amperes, the resistance would be 55 ohms.

Can Ohm’s Law be applied to all materials?

Ohm’s Law applies to many materials but not all. Materials that obey Ohm’s Law, where the resistance remains constant regardless of the voltage and current, are called ohmic materials. Non-ohmic materials, such as diodes or transistors, do not have a constant resistance, and their behavior cannot be accurately described by Ohm’s Law.

How does temperature affect Ohm’s Law?

Temperature can affect the resistance of a material. In most conductors, resistance increases with an increase in temperature. Therefore, as the temperature changes, the current and voltage relationship described by Ohm’s Law will also change if the resistance is not constant.

Can Ohm’s Law be used for AC circuits?

Ohm’s Law can be applied to AC (alternating current) circuits, but it must include impedance instead of just resistance. Impedance, denoted as 𝑍Z, is a more comprehensive measure that accounts for resistance, inductance, and capacitance in AC circuits. The formula then becomes 𝑉=𝐼𝑍.