The Superposition Principle is a fundamental concept in physics stating that, in a linear system, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. This principle applies across various domains of physics, including mechanics, electromagnetism, and Laws of quantum mechanics.
What is Superposition Principle?
The Superposition Principle states that in a linear system, the net response from two or more stimuli equals the sum of the responses each stimulus would have caused individually. This principle applies to various fields, including mechanics, electromagnetism, and quantum mechanics.
Formula of Superposition Principle
For a system where 𝑦 is the response and 𝑥₁,𝑥₂,…,𝑥ₙ are the individual stimuli, the superposition principle can be expressed as:
Principle of Superposition in Electrostatics
The superposition principle is particularly useful when dealing with numerous charges in a system. Let’s examine the following scenario:

For simplicity, consider one positive charge 𝑄 and two negative charges 𝑞₁ and 𝑞₂ exerting forces on it. According to the superposition theorem, the resultant force on 𝑄 is the vector sum of all individual forces. Therefore, the force 𝐹𝑟 can be expressed as:
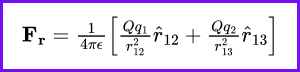
Where,
- 𝑟^₁₂ and 𝑟^₁₃ are the unit vectors in the direction of 𝑞₁ and 𝑞₂, respectively.
- 𝜖ϵ is the permittivity constant of the medium in which the charges are located.
- Q, 𝑞₁, and 𝑞₂ are the magnitudes of the charges.
- 𝑟₁₂ and 𝑟₁₃ are the distances between the charge Q and the charges 𝑞₁ and 𝑞₂, respectively.
Uses of Superposition Principle
- Electromagnetism: In electrostatics, the superposition principle determines the total electric field from multiple charges by summing the individual fields. It also calculates the net magnet field from several current-carrying conductors by adding their individual fields.
- Mechanics: The principle explains wave interfere by summing the displacements from overlapping waves, leading to phenomena like constructive and destructive interfere. Engineers use it in structural analysis to find deflection and stresses by breaking problems into simpler parts.
- Quantum Mechanics: In quantum mechanics, the principle states that a system can exist in all possible states simultaneously. It helps describe the probability amplitude of a particle’s position and momentum, aiding predictions of particle behavior at the quantum level.
- Circuit Analysis: In electrical engineering, the superposition principle simplifies the analysis of linear circuits with multiple sources. By considering each source independent and summing their effects, engineers determine the overall voltage and current.
- Acoustics: In acoustics, the principle helps understand how different sound waves interact by summing pressure variations from individual sound waves to predict the resultant sound. This is crucial for designing concert halls and auditoriums.
- Optics: In optics, the principle explains the interference and diffraction of light. When light waves overlap, the superposition of their electric fields determines the resultant intensity and pattern, essential for technologies like holography.
Examples for Superposition Principle
- Electric Fields: Calculating the electric field at a point due to multiple point charges. The superposition principle determines the resultant electric field by summing the individual electric fields produced by each charge. This method is essential for understanding complex electric field distributions in electrostatics.
- Wave Interference: Understanding the resultant displacement of overlap water waves. The superposition principle explains constructive and destructive interfere by summing the displacements from each wave, crucial for studying wave behaviors in mediums like water and air.
- Quantum Mechanics: Describing the quantum states of particles. The superposition principle states that a particle can exist in multiple states simultaneously. This concept is fundamental in quantum mechanics, enable predictions of particle behavior and quantum state evolution.
- Circuit Analysis: Simplifying the analysis of electrical circuits with multiple sources. Engineers use the superposition principle to find the overall voltage and current by considering each source independently and then summing their effects. This approach is vital for designing and analyze complex electrical circuits.
- Acoustics: Analyzing sound wave interactions. The superposition principle helps predict the result sound wave by summing the pressure variations from individual sound waves. This principle is crucial for designing auditoriums, concert halls, and other spaces require precise acoustic properties.
- Optics: Explaining light wave interfere and diffraction patterns. The superposition principle determines the result intensity and pattern when light waves overlap, essential for technologies like holography and for understanding optical phenomena.
FAQ’s
The principle is fundamental in physics and was formalized by many scientists, notably in wave theory and quantum mechanics.
In signal processing, superposition allows the combination and analysis of multiple signals.
The net force acting on an object is the vector sum of all individual forces applied.
Yes, quantum superposition states that particles can exist in multiple states simultaneously until measured.
Superposition allows the general solution of linear differential equations to be the sum of particular solutions.
Superposition holds true in linear systems where responses are directly proportional to inputs.
Yes, mechanical systems like vibrate strings and membranes exhibit superposition when multiple forces act simultaneously.
Superposition creates interference patterns, with constructive interference amplifying and destructive interfere reducing wave amplitudes.
Yes, in electrostatics, the net electric field is the vector sum of the individual fields produced by each charge.
In waves, the superposition principle means the resultant wave amplitude is the sum of the individual wave amplitudes.



