Notations
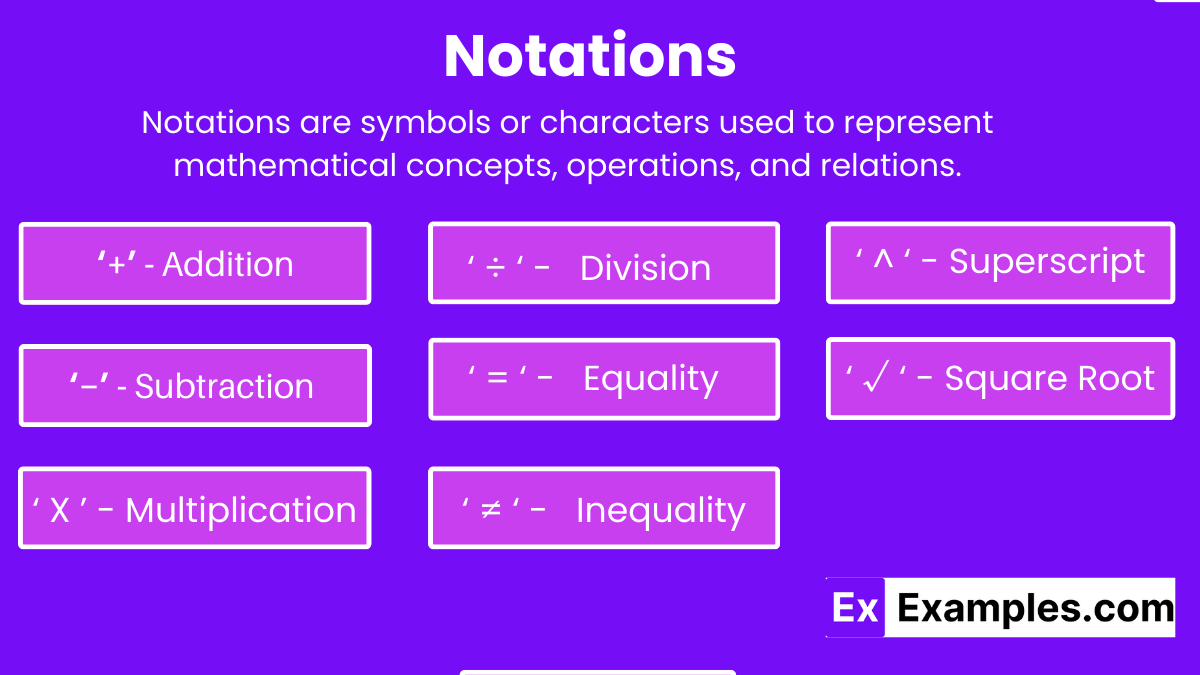
Notations are symbolic representations used to denote numbers, operations, functions, sets, and various mathematical concepts. They provide a concise and precise way to express complex ideas, making communication and problem-solving more efficient. Standard notations include numerals (0-9), operation symbols (Addition, Subtraction, Multiplication, Division), and function symbols (f(x), sin, log). Notations are essential in all areas of mathematics, from basic arithmetic to advanced calculus and abstract algebra. Understanding and using correct notations is crucial for mathematical literacy and effective communication among students, educators, and professionals.
What is Notation?
Notation in mathematics is a system of symbols and signs used to represent numbers, operations, functions, and other mathematical concepts. It serves as a universal language that simplifies complex ideas and facilitates clear communication. Common examples include numerals (1, 2, 3), operational symbols (+, -, ×, ÷), and function symbols (f(x), sin, log). Proper understanding and usage of notation are essential for problem-solving and advancing in mathematical studies.
Notation History
Ancient Civilizations
Ancient civilizations, such as the Egyptians and Babylonians, developed some of the earliest notations. The Egyptians used hieroglyphs to represent numbers, while the Babylonians employed a base-60 system using cuneiform symbols.
Greek Contributions
The Greeks introduced alphabetic notations and symbols to represent mathematical concepts, such as pi (π) for the ratio of a circle’s circumference to its diameter. Euclid’s “Elements” played a pivotal role in formalizing these notations.
Roman Numerals
The Romans developed a numeral system based on letters of the Latin alphabet (I, V, X, L, C, D, M) to represent numbers. This system was widely used across the Roman Empire and influenced medieval Europe.
Medieval Advancements
During the Middle Ages, scholars in the Islamic world made significant contributions to mathematical notation, including the introduction of Arabic numerals (0-9) and the decimal positional system, which revolutionized calculations.
Renaissance Developments
The Renaissance period saw the standardization of various notations. Mathematicians like François Viète and René Descartes introduced symbols for unknowns and constants, laying the groundwork for algebraic notation.
Modern Notation
In the 17th century, mathematicians like Isaac Newton and Gottfried Wilhelm Leibniz developed calculus notations. The 18th and 19th centuries saw further standardization, with Leonard Euler’s contributions to function notation (f(x)), and the introduction of matrix and set notations.
20th Century and Beyond
The 20th century brought the formalization of symbolic logic and the development of notations for abstract algebra, computer science, and other advanced fields. Modern notation continues to evolve, reflecting the expanding scope of mathematical research.
Notation in Math’s
Mathematical notation is a system of symbols used to represent numbers, operations, relations, and other mathematical concepts. It provides a universal language for mathematicians to communicate ideas clearly and concisely. Common symbols include numerals (0-9), operational signs (Addition, Subtraction, Multiplication, Division), and relational symbols (=, ≠, <, >). Variables (e.g., x, y) represent unknown values, while constants (e.g., π, e) have fixed values. Functions are denoted using letters like f(x) or g(x). Notation also extends to more complex structures such as matrices, vectors, and summation signs (Σ). Integers, algebra, and other advanced mathematical concepts rely heavily on precise notation for solving equations, proving theorems, and performing calculations, ensuring precision and avoiding ambiguity. Proper use of notation is crucial for mathematical literacy and effective communication among students, educators, and professionals. It plays a foundational role in all branches of mathematics, from elementary arithmetic to advanced calculus and beyond.
Types of Notations in Mathematics
| Type of Notation | Description |
|---|---|
| Symbolic Notation | Uses symbols to represent numbers, operations, and relations (e.g., +, -, =). |
| Algebraic Notation | Represents variables and constants using letters and symbols (e.g., x, y, a). |
| Geometric Notation | Uses figures, points, lines, and angles to represent geometric concepts. |
| Set Notation | Describes sets and their elements (e.g., {a, b, c}, N, ∅). |
| Functional Notation | Represents functions and their mappings (e.g., f(x), g(y)). |
| Matrix Notation | Uses arrays to represent matrices (e.g., A, B). |
| Vector Notation | Denotes vectors using bold letters or arrows (e.g., 𝑣v, 𝑣⃗v). |
| Calculus Notation | Involves derivatives and integrals (e.g., 𝑑𝑦𝑑𝑥dxdy, ∫f(x)dx). |
| Logical Notation | Represents logical operations and quantifiers (e.g., ∧, ∨, ∀, ∃). |
| Complex Number Notation | Uses the form 𝑎+𝑏𝑖 to represent complex numbers. |
Top 10 Mathematical Notations
- + – Addition
- − – Subtraction
- × – Multiplication
- ÷ – Division
- = – Equality
- ≠ – Inequality
- ^ – Superscript
- √ – Square Root
- π – Pi
- Σ – Summation
Basic Maths Notations
| Notation | Symbol | Description | Example |
|---|---|---|---|
| Addition | + | Operation of adding two numbers or expressions | 3+4=73+4=7 |
| Subtraction | − | Operation of subtracting one number or expression from another | 9−5=49−5=4 |
| Multiplication | × or ⋅ | Operation of multiplying two numbers or expressions | 6×3=186×3=18 or 6⋅3=186⋅3=18 |
| Division | ÷ or / | Operation of dividing one number by another | 12÷4=312÷4=3 or 12/4=312/4=3 |
| Equality | = | Shows that two expressions are equal in value | 2+2=42+2=4 |
| Inequality | ≠, <, >, ≤, ≥ | Represents relationships where expressions are not equal or one is greater/less than the other | 5≠35=3, 4<74<7, 9>29>2 |
| Exponentiation | ^ or superscript | Indicates raising a number to a power | 32=932=9 |
| Square Root | √ | Represents the square root of a number | √16=4√16=4 |
| Fraction | / or 𝑎𝑏ba | Represents the division of two numbers | 12=0.521=0.5 |
| Percentage | % | Represents a number as a fraction of 100 | 50%=5010050%=10050 = 0.5 |
What is the notation for summation?
The notation for summation is the Greek letter Sigma (Σ), representing the sum of a sequence of numbers.
How is factorial notation represented?
Factorial notation is represented by an exclamation mark (n!), which signifies the product of all positive integers up to n.
What does the notation ∫ represent?
The notation ∫ represents the integral sign, used to denote integration in calculus.
What is the notation for the derivative of a function?
The derivative of a function is commonly denoted by 𝑓′(𝑥) or 𝑑𝑦/𝑑𝑥
How do you represent complex numbers in notation?
Complex numbers are represented as 𝑎+𝑏𝑖, where 𝑎 is the real part and 𝑏𝑖 is the imaginary part.
What is the notation for the set of all natural numbers?
The set of all natural numbers is denoted by N.
How are matrices notated in mathematics?
Matrices are usually denoted by uppercase bold letters such as A, B, etc.
What notation is used for vectors?
Vectors are typically denoted by lowercase bold letters such as 𝑣v or with an arrow above the letter, like v.
How is the absolute value of a number notated?
The absolute value of a number 𝑥x is denoted by ∣x∣.
How is the empty set notated?
The empty set is notated by ∅ or {}
Share :
