Density
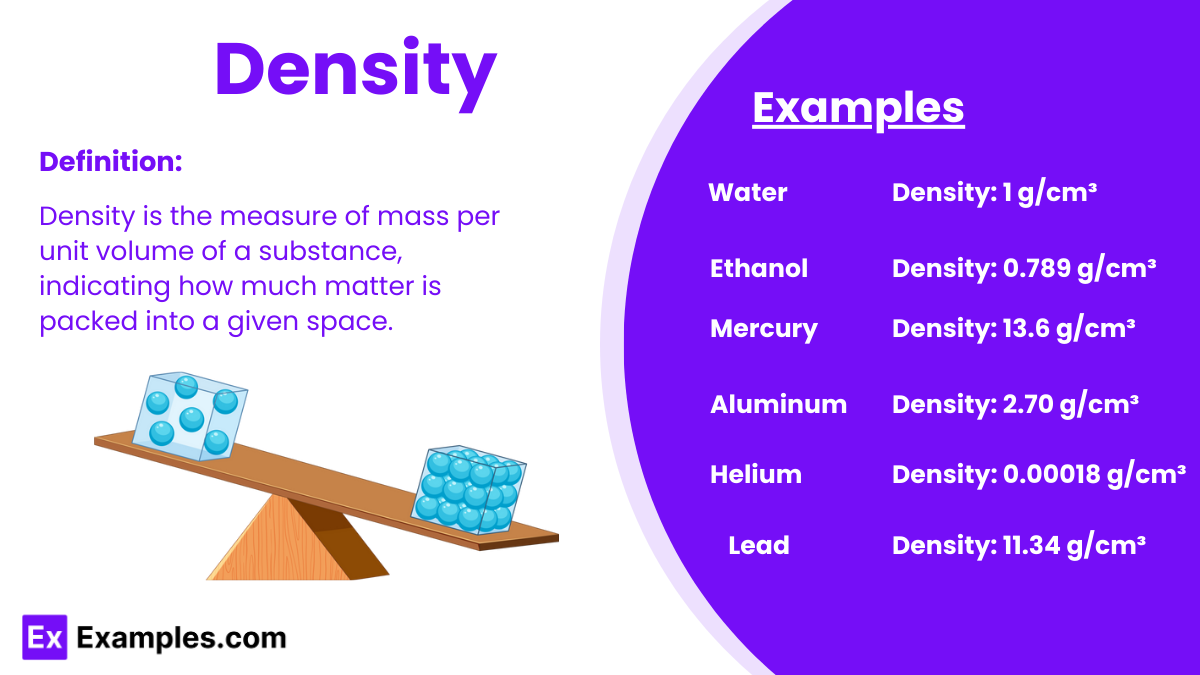
Understanding the concept of density is crucial for mastering various topics in AP Physics, including fluids, buoyancy, and material properties. Below are detailed notes to help you achieve a high score on your AP Physics exam.
Learning Objectives
Understand the concept of density, its definition, and mathematical formula. Learn how to calculate density using mass and volume, and comprehend its units (kg/m³ or g/cm³). Apply density principles to solve problems involving buoyancy, fluid mechanics, and material properties. Analyze and interpret density-related data in various contexts, including experimental measurements. Recognize the significance of density in real-world applications and its relevance to the AP Physics exam. Develop proficiency in solving complex problems involving density variations in different states of matter.
Definition of Density
Density (ρ): Density is defined as the mass per unit volume of a substance. It is a measure of how much mass is contained in a given volume.
Formula: \[ \rho = \frac{m}{V} \]
where:
- ρ is the density (in kg/m³ or g/cm³),
- m is the mass (in kg or g),
- V is the volume (in m³ or cm³).
Key Points:
- Density is a scalar quantity.
- Different substances have different densities, which can be used to identify materials.
Units of Density
SI Unit:
- Kilograms per cubic meter (kg/m³)
Common Unit:
- Grams per cubic centimeter (g/cm³)
Conversion between Units
To convert from g/cm³ to kg/m³, multiply by 1000:
1 g/cm³ = 1000 kg/m³
Calculating Density
Example 1: Solid Object
Scenario: A metal cube has a mass of 200 g and a volume of 50 cm³. Calculate its density.
Solution:
\[ \rho = \frac{m}{V} \] \[ \rho = \frac{200 \, \text{g}}{50 \, \text{cm}^3} \] \[ \rho = 4 \, \text{g/cm}^3 \]
Example 2: Liquid
Scenario: A container holds 500 mL of a liquid with a mass of 600 g. Calculate the density of the liquid.
Solution: First, convert volume from mL to cm³ (since 1 mL = 1 cm³): V = 500cm³
Now, calculate the density:
\[ \rho = \frac{m}{V} \] \[ \rho = \frac{600 \, \text{g}}{500 \, \text{cm}^3} \] \[ \rho = 1.2 \, \text{g/cm}^3 \]
Problem 2: Finding Mass Using Density
Question:
A liquid has a density of 1.2 g/cm³. What is the mass of 250 cm³ of this liquid?
Solution:
Mass = Density × Volume
Mass = 1.2 g/cm³ × 250 cm³
Mass = 300 g
Applications of Density
Buoyancy
Buoyancy: The buoyant force on an object submerged in a fluid is equal to the weight of the fluid displaced by the object. This principle is described by Archimedes’ principle.
Formula: \[ F_b = \rho_f V_f g \]
where:
- Fb is the buoyant force,
- ρբ is the density of the fluid,
- Vբ is the volume of the fluid displaced,
- g is the acceleration due to gravity.
Example: Buoyant Force on a Submerged Object
Scenario: A block of wood with a density of 0.6 g/cm³ and a volume of 1000 cm³ is submerged in water. Calculate the buoyant force acting on the block.
Solution: First, convert the density of the block to kg/m³:
ρblock = 0.6g/cm³×1000 = 600kg/m³
Density of water: ρᵥᵥₐₜₑᵣ = 1000kg/m³
Volume of the block: Vblock = 1000cm³ = 0.001m³
Buoyant force: \[ F_b = \rho_{\text{water}} V_{\text{block}} g \]
\[ F_b = 1000 \, \text{kg/m}^3 \times 0.001 \, \text{m}^3 \times 9.8 \, \text{m/s}^2 \]
\[ F_b = 9.8 \, \text{N} \]
Specific Gravity
Specific Gravity: Specific gravity is the ratio of the density of a substance to the density of a reference substance (usually water for liquids and solids).
Formula: \[\text{Specific Gravity} = \frac{\rho_{\text{substance}}}{\rho_{\text{water}}}\]
Key Points:
- Specific gravity is a dimensionless quantity.
- For liquids and solids, water at 4°C is typically used as the reference substance.
Example: Specific Gravity
Scenario: A sample of oil has a density of 0.8 g/cm³. Calculate its specific gravity.
Solution: Density of water: ρwater=1g/cm3
\[\text{Specific Gravity} = \frac{\rho_{\text{oil}}}{\rho_{\text{water}}} \\ \text{Specific Gravity} = \frac{0.8 \, \text{g/cm}^3}{1 \, \text{g/cm}^3} \\ \text{Specific Gravity} = 0.8\]
Practice Problems
Question 1:
A block of wood has a mass of 600 grams and a volume of 800 cm³. What is the density of the wood?
A) 0.5 g/cm³
B) 0.75 g/cm³
C) 1.0 g/cm³
D) 1.25 g/cm³
Answer: B) 0.75 g/cm³
Explanation:
Density ρ is defined as mass per unit volume and is calculated using the formula:
\[ \rho = \frac{m}{V} \]
Given:
- Mass m = 600g
- Volume V = 800cm³
Calculate the density:
\[\rho = \frac{600 \, \text{g}}{800 \, \text{cm}^3} = 0.75 \, \text{g/cm}^3\]
Thus, the correct answer is 0.75 g/cm³.
Question 2:
A liquid has a density of 1.2 g/cm³. What is the mass of 500 cm³ of this liquid?
A) 420 g
B) 500 g
C) 600 g
D) 720 g
Answer: C) 600 g
Explanation:
The mass m of a substance can be calculated using the formula:
m = ρ×V
Given:
- Density ρ = 1.2g/cm³
- Volume V = 500cm³
Calculate the mass:
m = 1.2g/cm³×500cm³ = 600g
Thus, the correct answer is 600 g.
Question 3:
Which of the following statements is true if a solid object has a density greater than that of water?
A) The object will float in water.
B) The object will sink in water.
C) The object will neither float nor sink.
D) The object’s density is irrelevant to its buoyancy.
Answer: B) The object will sink in water.
Explanation:
According to the principle of buoyancy, an object will float in a fluid if its density is less than the density of the fluid. Conversely, an object will sink if its density is greater than the density of the fluid.
Given that the density of the solid object is greater than that of water, the object will sink.
Thus, the correct answer is the object will sink in water.