Thermodynamics and Collisions

Understanding the principles of thermodynamics and collisions is crucial for mastering key concepts in physics and achieving a high score on the AP Physics exam. Thermodynamics deals with heat, work, and energy transformations, while collisions focus on momentum and energy exchanges during interactions between objects. Below are detailed notes along with five examples to help you excel in these topics.

Learning Objectives

In the topic of Thermodynamics for the AP Physics exam, you should learn the laws of thermodynamics, heat transfer methods, and the principles of energy conservation in thermodynamic processes. For Collisions, focus on understanding momentum conservation, different types of collisions (elastic and inelastic), and kinetic energy transformations. Grasp the mathematical formulations and applications of these principles to solve real-world physics problems efficiently. Mastery of these topics will prepare you for both conceptual and quantitative questions on the exam.

Thermodynamics

First Law of Thermodynamics

First Law of Thermodynamics: The first law of thermodynamics states that the change in the internal energy of a system is equal to the heat added to the system minus the work done by the system.

Equation: ΔU = Q−W

where:

• ΔU is the change in internal energy,
• Q is the heat added to the system,
• W is the work done by the system.

Key Points:

• Heat added to the system increases internal energy.
• Work done by the system decreases internal energy.

Second Law of Thermodynamics

Second Law of Thermodynamics: The second law of thermodynamics states that the total entropy of an isolated system can never decrease over time. It can remain constant in ideal cases where the system is in a reversible process, but it must increase for irreversible processes.

Key Points:

• Entropy is a measure of disorder or randomness.
• Heat naturally flows from hot to cold bodies.

Heat Engines and Efficiency

Heat Engine: A heat engine is a device that converts heat into work by using a working substance, typically undergoing a cyclic process.

Efficiency (η): The efficiency of a heat engine is the ratio of the work output to the heat input.

Equation: \[ \eta = \frac{W}{Q_H} = 1 – \frac{Q_C}{Q_H} \]

where:

• W is the work done by the engine,
• Qₕ​ is the heat absorbed from the hot reservoir,
• Q꜀​ is the heat released to the cold reservoir.

Collisions

Types of Collisions

Elastic Collision: A collision in which both momentum and kinetic energy are conserved.

Inelastic Collision: A collision in which momentum is conserved, but kinetic energy is not conserved. Some kinetic energy is transformed into other forms of energy.

Conservation of Momentum

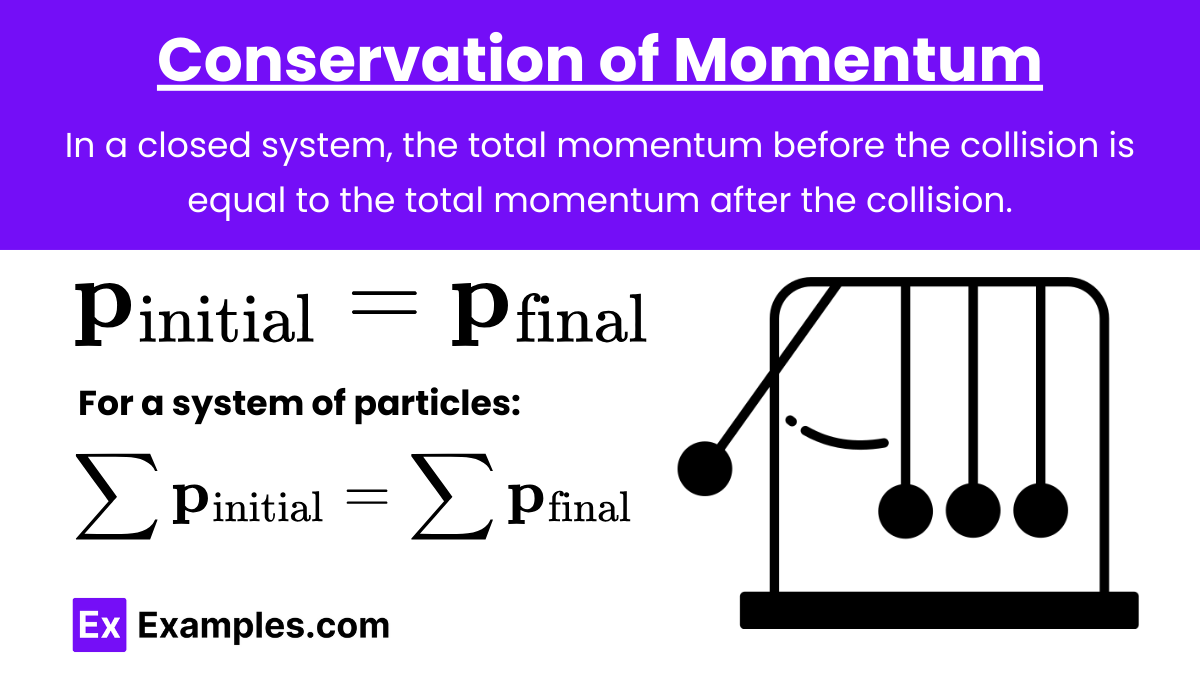
Conservation of Momentum: In a closed system, the total momentum before the collision is equal to the total momentum after the collision.

Equation: \[ \mathbf{p}_{\text{initial}} = \mathbf{p}_{\text{final}} \] \[ m_1 \mathbf{v}_{1i} + m_2 \mathbf{v}_{2i} = m_1 \mathbf{v}_{1f} + m_2 \mathbf{v}_{2f} \]

Conservation of Kinetic Energy (Elastic Collisions)

Equation: ​\[ \frac{1}{2} m_1 v_{1i}^2 + \frac{1}{2} m_2 v_{2i}^2 = \frac{1}{2} m_1 v_{1f}^2 + \frac{1}{2} m_2 v_{2f}^2 \]

Examples

Example 1: First Law of Thermodynamics

Scenario: A gas undergoes an expansion, doing 150 J of work on its surroundings while 200 J of heat is added to the gas. Calculate the change in internal energy.

Solution: ΔU = Q−W
ΔU = 200J−150J = 50J

Example 2: Efficiency of a Heat Engine

Scenario: A heat engine absorbs 500 J of heat from the hot reservoir and releases 300 J to the cold reservoir. Calculate the efficiency of the engine.

Solution: \[ \eta = 1 – \frac{Q_C}{Q_H} \] \[ \eta = 1 – \frac{300 \, \text{J}}{500 \, \text{J}} = 1 – 0.6 = 0.4 \] \[ \eta = 40\% \]

Example 3: Elastic Collision

Scenario: Two identical carts collide elastically on a frictionless track. Cart A (1 kg) moves at 2 m/s towards Cart B (1 kg) at rest. Calculate their velocities after the collision.

Solution: Using conservation of momentum and kinetic energy:
\[ m_1 v_{1i} + m_2 v_{2i} = m_1 v_{1f} + m_2 v_{2f} \] \[ 1 \times 2 + 1 \times 0 = 1 \times v_{1f} + 1 \times v_{2f} \] \[ 2 = v_{1f} + v_{2f} \] \[ \frac{1}{2} m_1 v_{1i}^2 + \frac{1}{2} m_2 v_{2i}^2 = \frac{1}{2} m_1 v_{1f}^2 + \frac{1}{2} m_2 v_{2f}^2 \] \[ \frac{1}{2} \times 1 \times 2^2 + 0 = \frac{1}{2} \times 1 \times v_{1f}^2 + \frac{1}{2} \times 1 \times v_{2f}^2 \] \[ 2 = \frac{1}{2} v_{1f}^2 + \frac{1}{2} v_{2f}^2 \] \[ 4 = v_{1f}^2 + v_{2f}^2 \] \[\text{Solving the system of equations:}\] \[ v_{1f} = 0 \, \text{m/s}, \, v_{2f} = 2 \, \text{m/s} \]

Example 4: Inelastic Collision

Scenario: A 3 kg ball moving at 4 m/s collides with a 2 kg ball at rest. They stick together. Calculate the velocity of the combined mass after the collision.

Solution: \[ m_1 v_{1i} + m_2 v_{2i} = (m_1 + m_2) v_f \] \[ 3 \times 4 + 2 \times 0 = (3 + 2) v_f \] \[ 12 = 5 v_f \] \[ v_f = \frac{12}{5} = 2.4 \, \text{m/s} \]

Example 5: Second Law of Thermodynamics

Scenario: A refrigerator extracts 600 J of heat from its interior and expels 800 J to the surroundings. Calculate the work done by the refrigerator.

Solution: W = Qₕ​−Q꜀
W = 800J−600J = 200J

Practice Problems

Question 1:

An ideal gas undergoes an isothermal expansion at a temperature of 300 K. If the initial volume of the gas is 1 L and the final volume is 3 L, what is the ratio of the final pressure to the initial pressure?

A) 1:3
B) 3:1
C) 1:9
D) 9:1

Answer: A) 1:3

Explanation:

For an isothermal process (constant temperature), the ideal gas law PV=nRT implies that P∝1/V since nRT is constant. Therefore, the relationship between initial and final states can be expressed as:

P₁​V₁ ​= P₂​V₂

Given:

• V₁ ​= 1L
• V₂ = 3L

We need to find the ratio of P₂​ to P₁​:

\[ P_1 \times 1 \, \text{L} = P_2 \times 3 \, \text{L} \] \[ P_2 = \frac{P_1}{3} \]

So, the ratio of the final pressure to the initial pressure is:

\[ \frac{P_2}{P_1} = \frac{1}{3} \]

Thus, the correct answer is 1:3.

Question 2:

In a perfectly elastic collision, a 2 kg ball moving at 3 m/s collides head-on with a stationary 4 kg ball. What is the speed of the 2 kg ball after the collision?

A) 1 m/s
B) 2 m/s
C) -1 m/s
D) 0 m/s

Answer: C) -1 m/s

Explanation:

In a perfectly elastic collision, both momentum and kinetic energy are conserved. For two objects colliding head-on, the velocities after collision can be determined using the following equations for perfectly elastic collisions:

\[ v_{1f} = \frac{(m_1 – m_2)v_{1i} + 2m_2v_{2i}}{m_1 + m_2} \] \[ v_{2f} = \frac{(m_2 – m_1)v_{2i} + 2m_1v_{1i}}{m_1 + m_2} \]

Given:

\[ m_1 = 2 \, \text{kg} \] \[ m_2 = 4 \, \text{kg} \] \[ v_{1i} = 3 \, \text{m/s} \] \[ v_{2i} = 0 \, \text{m/s} \]

Substitute these values into the equation for v₁f​:

\[ v_{1f} = \frac{(2 – 4) \times 3 + 2 \times 4 \times 0}{2 + 4} \] \[ v_{1f} = \frac{-6}{6} = -1 \, \text{m/s} \]

Thus, the speed of the 2 kg ball after the collision is -1 m/s, indicating it reverses direction.

Question 3:

A Carnot engine operates between a high-temperature reservoir at 500 K and a low-temperature reservoir at 300 K. What is the efficiency of the Carnot engine?

A) 40%
B) 50%
C) 60%
D) 70%

Answer: A) 40%

Explanation:

The efficiency η of a Carnot engine is given by the formula:

\[ \eta = 1 – \frac{T_C}{T_H} \]

where T꜀ is the temperature of the cold reservoir and Tₕ​ is the temperature of the hot reservoir.

Given:

• Tₕ​ = 500K
• T꜀ ​= 300K

Substitute these values into the efficiency equation:

\[ \eta = 1 – \frac{300 \, \text{K}}{500 \, \text{K}} \] \[ \eta = 1 – 0.6 = 0.4 \]

Converting to percentage:

η = 0.4×100% = 40%

Thus, the efficiency of the Carnot engine is 40%.