Properties of Waves and Particles

Understanding the Properties of Waves and Particles is fundamental in physics, especially for the AP Physics exam. Waves, including mechanical and electromagnetic types, exhibit characteristics like wavelength, frequency, and speed. Particles display mass and charge, and in quantum mechanics, they also exhibit wave-like behaviors. The wave-particle duality, demonstrated by experiments like the double-slit and photoelectric effect, bridges classical and quantum physics, essential for comprehending modern technological applications and advancements.

Learning Objectives

Focus on understanding the characteristics and behavior of mechanical and electromagnetic waves, including wavelength, frequency, amplitude, and speed. Grasp the principles of wave-particle duality, demonstrated through key experiments like the double-slit experiment and the photoelectric effect. Learn the De Broglie hypothesis and Heisenberg Uncertainty Principle, and explore applications of wave-particle duality in quantum mechanics and modern technology, such as semiconductors and medical imaging.

1. Waves

Waves are disturbances that transfer energy through space and matter without transferring matter itself. There are two main types of waves: mechanical waves and electromagnetic waves.

A. Mechanical Waves

• Definition: Waves that require a medium to travel through, such as sound waves, water waves, and seismic waves.
• Types:
  • Transverse Waves: The oscillation is perpendicular to the direction of the wave propagation (e.g., water waves, waves on a string).
  • Longitudinal Waves: The oscillation is parallel to the direction of the wave propagation (e.g., sound waves).

Properties of Mechanical Waves:

• Wavelength (λ): The distance between consecutive crests or troughs in a wave.
• Frequency (f): The number of waves that pass a given point per second, measured in Hertz (Hz).
• Amplitude: The maximum displacement from the rest position.
• Speed (v): The speed at which the wave propagates through the medium, given by v = fλ.

B. Electromagnetic Waves

• Definition: Waves that do not require a medium and can travel through a vacuum, such as light, radio waves, and X-rays.
• Nature: Composed of oscillating electric and magnetic fields that propagate perpendicular to each other and to the direction of the wave.

Properties of Electromagnetic Waves:

• Wavelength and Frequency: Similar to mechanical waves, but they travel at the speed of light 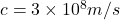in a vacuum.
• Spectrum: Includes radio waves, microwaves, infrared, visible light, ultraviolet, X-rays, and gamma rays, ordered by increasing frequency and decreasing wavelength.

2. Particles

Particles are small localized objects that can be described by physical properties such as mass, charge, and volume. In classical physics, particles are considered to have well-defined positions and velocities.

A. Classical Particles

• Examples: Atoms, molecules, electrons, protons, and neutrons.
• Properties:
  • Mass: The amount of matter in a particle.
  • Charge: Electric charge (positive or negative).
  • Momentum (p): The product of mass and velocity, given by p = mv.

B. Quantum Particles

• In quantum mechanics, particles also exhibit wave-like properties, leading to the concept of wave-particle duality.

3. Wave-Particle Duality

• Principle: Particles such as electrons and photons exhibit both wave-like and particle-like properties depending on the experiment conducted.
• Key Experiments:
  • Double-Slit Experiment: Demonstrates the wave nature of particles through interference patterns.
  • Photoelectric Effect: Demonstrates the particle nature of light, where light incident on a material ejects electrons, explained by photons (particles of light) imparting energy to the electrons.

A. De Broglie Hypothesis

• Proposed that particles, like electrons, have a wavelength associated with them, given by λ = ​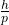, where h is Planck’s constant and p is the momentum.

B. Heisenberg Uncertainty Principle

• States that it is impossible to simultaneously know the exact position and momentum of a particle. The more precisely one property is known, the less precisely the other can be known, expressed as ΔxΔp≥​.

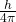4. Applications

A. Quantum Mechanics

• Understanding Matter and Energy: Wave-particle duality is foundational in quantum mechanics, explaining the behavior of particles at atomic and subatomic levels.
• Quantum Tunneling: Utilized in phenomena where particles pass through barriers they classically shouldn’t, essential in nuclear fusion and scanning tunneling microscopes.

B. Technology

• Semiconductors: Leveraging electron behavior for developing electronic devices like transistors, diodes, and integrated circuits, fundamental to modern electronics.
• Lasers: Based on stimulated emission, crucial for applications in communication, medicine, and industry.
• Quantum Computing: Exploiting quantum states for processing information exponentially faster than classical computers.

C. Medical Imaging

• MRI (Magnetic Resonance Imaging): Uses principles of nuclear magnetic resonance to create detailed images of the body’s internal structures.
• PET Scans (Positron Emission Tomography): Utilizes particle interactions to visualize metabolic processes in the body, aiding in diagnosis and research.

D. Communication

• Fiber Optics: Uses light waves for high-speed data transmission over long distances with minimal loss, revolutionizing telecommunications.
• Wireless Technology: Employs electromagnetic waves for transmitting information without physical connections, enabling mobile and satellite communications.

Examples of Properties of Waves and Particles

1. Double-Slit Experiment: Demonstrates the wave-like interference pattern of particles like electrons, highlighting wave-particle duality.
2. Photoelectric Effect: Shows the particle nature of light, where photons knock electrons out of a material, providing evidence of quantized energy levels.
3. Electron Diffraction: When electrons pass through a crystal lattice, they produce an interference pattern, confirming their wave properties.
4. X-ray Diffraction: Used to determine the atomic structure of crystals, exploiting the wave nature of X-rays.
5. Compton Scattering: Observes the change in wavelength of X-rays when they collide with electrons, demonstrating both wave and particle properties.

Practice Test Questions on Properties of Waves and Particles

1. Which of the following experiments demonstrates the wave nature of particles?

A. Photoelectric Effect
B. Double-Slit Experiment
C. Compton Scattering
D. Rutherford Gold Foil Experiment

Answer: B. Double-Slit Experiment

Explanation: The Double-Slit Experiment demonstrates the wave nature of particles by showing interference patterns when particles like electrons pass through two slits. If particles were purely particle-like, they would produce two distinct impact patterns corresponding to the slits. Instead, the interference pattern observed is characteristic of wave behavior, thus confirming wave-particle duality.

2. What property of light is highlighted by the photoelectric effect?

A. Wave Interference
B. Diffraction
C. Particle Nature
D. Polarization

Answer: C. Particle Nature

Explanation: The photoelectric effect demonstrates the particle nature of light. When light shines on a material, it ejects electrons from the surface. This effect can only be explained if light is considered to be made of particles called photons, each with a quantized amount of energy, which transfer energy to electrons, causing their ejection from the material.

3. According to de Broglie’s hypothesis, what determines the wavelength of a particle?

A. Its charge
B. Its mass
C. Its speed
D. Its momentum

Answer: D. Its momentum

Explanation: According to de Broglie’s hypothesis, the wavelength (λ) of a particle is inversely proportional to its momentum (p), given by the equation λ=h/p​, where h is Planck’s constant. This hypothesis extends wave-particle duality to all matter, suggesting that particles with greater momentum have shorter wavelengths, demonstrating their wave-like properties.