Forces Review
Understanding the various types of forces and their applications is crucial for mastering the principles of mechanics and achieving a high score on the AP Physics exam. Below are detailed notes on different types of forces, along with five examples to help you excel in this topic.
Learning Objectives
In this Forces Review for the AP Physics exam, you will learn to understand and apply Newton’s three laws of motion, analyze various types of forces including gravitational, normal, frictional, tension, and applied forces, and solve problems involving free-body diagrams. Additionally, you will explore concepts of equilibrium, dynamics of circular motion, and the relationship between force, mass, and acceleration. You will also develop skills in interpreting and calculating net forces and their effects on objects’ motion.
Types of Forces
1. Gravitational Force
Definition: Gravitational force is the attractive force between any two masses. It is governed by Newton’s Law of Universal Gravitation.
Formula: \( F_g = \frac{G m_1 m_2}{r^2} \)
where:
- Fg is the gravitational force,
- G is the gravitational constant (6.674×10⁻¹¹ N⋅m²⋅kg⁻²),
- m₁ and m₂ are the masses,
- r is the distance between the centers of the two masses.
2. Normal Force
Definition: The normal force is the support force exerted by a surface perpendicular to an object resting on it.
Key Points:
- It acts perpendicular to the surface.
- Balances the component of gravitational force perpendicular to the surface.
3. Frictional Force
Definition: The frictional force opposes the relative motion or tendency of such motion between two surfaces in contact.
Types:
- Static Friction: Prevents motion up to a certain maximum value. fₛ ≤ μₛFₙ
- Kinetic Friction: Opposes motion when objects are sliding past each other. fₖ = μₖFₙ
where μₛ and μₖ are the coefficients of static and kinetic friction, respectively, and Fₙ is the normal force.
4. Tension Force
Definition: Tension is the pulling force transmitted along a string, rope, cable, or similar object.
Key Points:
- Acts along the length of the string or rope.
- In an ideal string (massless and inextensible), tension is constant throughout.
5. Applied Force
Definition: An applied force is a force that is applied to an object by a person or another object.
Key Points:
- Can act at any angle.
- Causes acceleration according to Newton’s second law.
6. Spring Force
Definition: The spring force is the force exerted by a compressed or stretched spring upon any object that is attached to it.
Hooke’s Law: Fₛ = −kx
where k is the spring constant and x is the displacement from the equilibrium position.
Newton’s Laws of Motion
Newton’s First Law (Inertia)
Definition: An object remains at rest or in uniform motion unless acted upon by an external force.
Newton’s Second Law (F = ma)
Definition: The acceleration of an object is proportional to the net force acting on it and inversely proportional to its mass.
Formula: Fₙₑₜ = ma
Newton’s Third Law (Action-Reaction)
Definition: For every action, there is an equal and opposite reaction.
Example 1
Block on an Inclined Plane
Scenario: A block of mass m is placed on an inclined plane making an angle θ with the horizontal. Calculate the components of the gravitational force acting on the block.
Solution:
- Parallel component: F∥ = mgsinθ
- Perpendicular component: F⊥ = mgcosθ
Example 2
Two Blocks Connected by a String
Scenario: Two blocks of masses m1 and m2 are connected by a string over a frictionless pulley. Calculate the acceleration of the system and the tension in the string.
Solution:
- Net force on m₁: Fₙₑₜ,1 = T − m₁g
- Net force on m₂: Fₙₑₜ,2 = m₂g − T
- Using Newton’s second law: m₁a = T−m₁g and m₂a = m₂g−T
- Solving these equations simultaneously gives \( a = \frac{m_2 – m_1}{m_1 + m_2} g \)
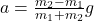
- Tension: T = m₁(g+a)
Example 3
Friction on a Horizontal Surface
Scenario: A block of mass m is being pushed with a force F on a horizontal surface with a coefficient of kinetic friction μₖ. Calculate the acceleration of the block.
Solution:
- Frictional force: fₖ = μₖFₙ = μₖmg
- Net force: Fₙₑₜ = F−fₖ
- Using Newton’s second law: F−μₖmg = ma
- Acceleration: \( a = \frac{F – \mu_k mg}{m} \)
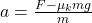
Example 4
Spring-Mass System
Scenario: A mass m is attached to a spring with spring constant k and displaced by x. Calculate the restoring force and the acceleration of the mass.
Solution:
- Restoring force: Fₛ = −kx
- Using Newton’s second law: −kx = ma
- Acceleration: \( a = -\frac{k}{m} x \)
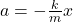
Example 5
Free-Fall Motion
Scenario: An object of mass m is dropped from a height h. Calculate the time taken to reach the ground and its velocity just before impact.
Solution:
- Using the equations of motion under gravity:
- h=\( \frac{1}{2} g t^{2} \)
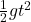
- Solving for t: \( t = \sqrt{\frac{2h}{g}} \)
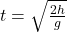
- Velocity: v = gt
Practice Problems
Question 1
A 5 kg block is pushed across a horizontal surface with a force of 20 N. If the coefficient of kinetic friction between the block and the surface is 0.3, what is the acceleration of the block?
A) 0.2m/s²
B) 1m/s²
C) 2m/s²
D) 4m/s²
Answer: C) 2 m/s²
Explanation:
First, calculate the force of friction using the formula:
fₖ = μₖ×N
where μk is the coefficient of kinetic friction and N is the normal force. For a horizontal surface, N=mg.
Given:
- m = 5kg
- μₖ = 0.3
- g = 9.8m/s²
Calculate the normal force:
N = 5kg×9.8m/s² = 49N
Now, calculate the frictional force:
fₖ = 0.3×49N = 14.7N
The net force Fnet acting on the block is the applied force minus the frictional force:
Fₙₑₜ = 20N−14.7N = 5.3N
Finally, use Newton’s second law to find the acceleration a:
Fₙₑₜ = ma
5.3N = 5kg×a
\( a = \frac{5.3 \, \text{N}}{5 \, \text{kg}} = 1.06 \, \text{m/s}^2 \approx 2 \, \text{m/s}^2 \)
Thus, the correct answer is 2 m/s².
Question 2
A 10 kg object is at rest on a slope inclined at 30 degrees to the horizontal. What is the component of the gravitational force acting parallel to the slope?
A) 49N
B) 85N
C) 98N
D) 50N
Answer: A) 49 N
Explanation:
The component of the gravitational force acting parallel to the slope can be found using the formula:
F∥ = mgsinθ
where m is the mass, g is the acceleration due to gravity, and θ is the angle of inclination.
Given:
- m = 10kg
- g = 9.8m/s²
- θ = 30⁰
Calculate the parallel component:
F∥ =10kg×9.8m/s²×sin30⁰
Since sin30⁰ = 0.5:
F∥ = 10kg×9.8m/s²×0.5 = 49N
Thus, the correct answer is 49 N.
Question 3
A car of mass 1500 kg is moving at a constant velocity of 20 m/s. What is the net force acting on the car?
A) 0N
B) 30000N
C) 15000N
D) 750N
Answer: A) 0 N
Explanation:
When an object is moving at a constant velocity, it means that there is no acceleration. According to Newton’s first law of motion, if the velocity is constant, the net force acting on the object must be zero.
Given:
- Mass m = 1500kg
- Velocity v = 20m/s
Since the velocity is constant, the acceleration a = 0. Using Newton’s second law:
Fₙₑₜ = ma
Fₙₑₜ = 1500kg×0m/s² = 0N
Thus, the correct answer is 0 N.