Gravitational and Electromagnetic Forces

Last Updated: September 24, 2024

Notes

Understanding gravitational and electromagnetic forces is crucial for mastering the concepts of forces and fields in the AP Physics exam. These fundamental forces govern interactions between masses and charges, respectively. Below are detailed notes along with five examples to help you achieve a high score on your AP Physics exam.

Free AP Physics 2: Algebra-Based Practice Test

Learning Objectives

In studying gravitational and electromagnetic forces for the AP Physics exam, you should understand the nature and properties of these fundamental forces, their similarities and differences, and how they govern the motion of objects. Learn to apply Newton’s Law of Universal Gravitation and Coulomb’s Law to calculate the forces, analyze electric and gravitational fields, and solve problems involving potential energy and work. Additionally, grasp the principles of superposition and the role of these forces in planetary motion and electromagnetic interactions.

Gravitational Forces

Newton’s Law of Universal Gravitation

Definition: Newton’s Law of Universal Gravitation states that every point mass attracts every other point mass in the universe with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

Formula:

$F_g = \frac{G m_1 m_2}{r^2}$

where:

Fg is the gravitational force between two masses,
G is the gravitational constant (6.674×10⁻¹¹ N⋅m²⋅kg⁻²6.674),
m₁ and m₂ are the masses of the two objects,
r is the distance between the centers of the two masses.

Key Points:

Gravitational force is always attractive.
It acts along the line joining the centers of the two masses.
It is a central force, depending only on the distance between the objects.

Gravitational Field

Definition: A gravitational field is a region of space surrounding a mass where another mass experiences a force of gravitational attraction.

Gravitational Field Strength:

$g = \frac{F_g}{m} = \frac{GM}{r^2}$

where:

g is the gravitational field strength,
M is the mass creating the gravitational field,
r is the distance from the mass.

Key Points:

Gravitational field strength decreases with the square of the distance from the mass.
It is a vector quantity, pointing towards the mass creating the field.

Electromagnetic Forces

Coulomb’s Law

Definition: Coulomb’s Law states that the electric force between two point charges is directly proportional to the product of the magnitudes of the charges and inversely proportional to the square of the distance between them.

Formula:

$F_e = k_e \frac{|q_1 q_2|}{r^2}$

where:

Fe is the electric force between two charges,
ke is Coulomb’s constant (8.9875×109 N⋅m²⋅C⁻²),
q₁ and q₂ are the magnitudes of the two charges,
r is the distance between the centers of the two charges.

Key Points:

Electric force can be attractive (opposite charges) or repulsive (like charges).
It acts along the line joining the centers of the two charges.
It is a central force, depending only on the distance between the objects.

Electric Field

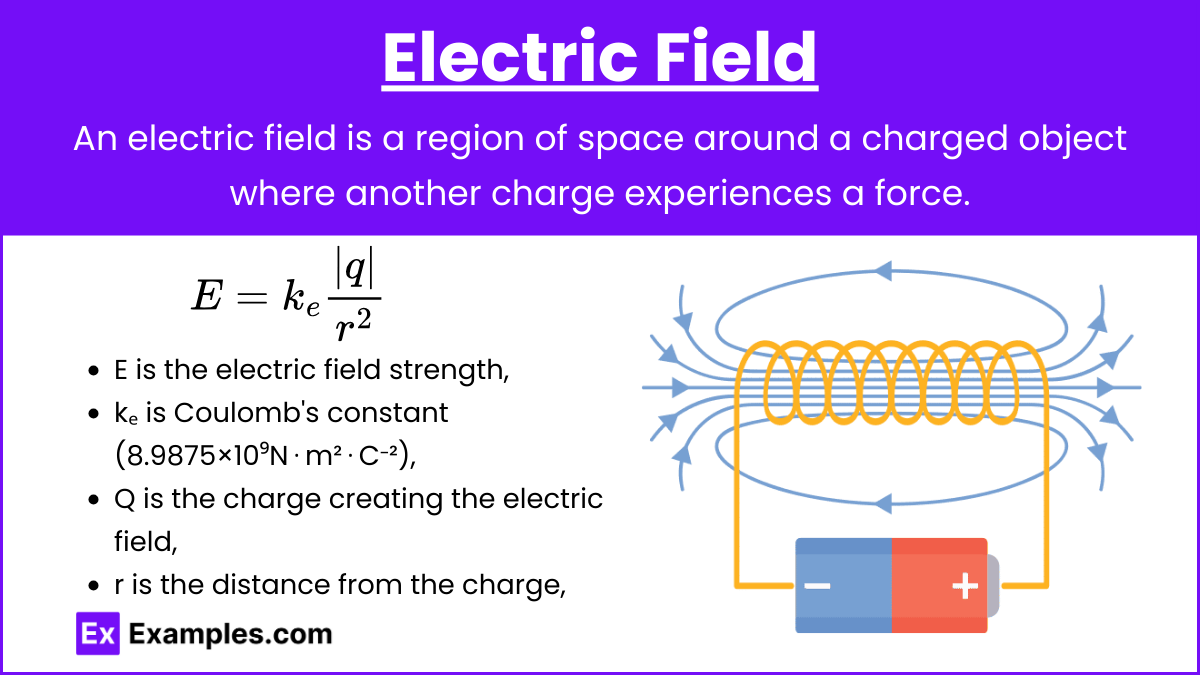
Definition: An electric field is a region of space around a charged object where another charge experiences a force.

Electric Field Strength:

$E = \frac{F_e}{q} = k_e \frac{Q}{r^2}$

where:

E is the electric field strength,
kₑ is Coulomb’s constant (8.9875×10⁹N⋅m²⋅C⁻²),
Q is the charge creating the electric field,
r is the distance from the charge.

Key Points:

Electric field strength decreases with the square of the distance from the charge.
It is a vector quantity, pointing away from positive charges and towards negative charges.

Example 1

Gravitational Force Between Two Masses

Scenario: Calculate the gravitational force between two 10 kg masses separated by a distance of 2 meters.

Solution:

$F_g = \frac{G m_1 m_2}{r^2}$

$F_g = \frac{6.674 \times 10^{-11} \times 10 \times 10}{2^2}$

$F_g = \frac{6.674 \times 10^{-11} \times 100}{4}$

$F_g = 1.6685 \times 10^{-9} \, \text{N}$

Example 2

Electric Force Between Two Charges

Scenario: Calculate the electric force between two charges of +3μC and −3μC separated by a distance of 1 meter.

Solution:

$F_e = k_e \frac{|q_1 q_2|}{r^2}$

$F_e = 8.9875 \times 10^9 \frac{3 \times 10^{-6} \times 3 \times 10^{-6}}{1^2}$

$F_e = 8.9875 \times 10^9 \times 9 \times 10^{-12}$

$F_e = 8.09 \times 10^{-2} \, \text{N}$

Example 3

Gravitational Field Strength

Scenario: Calculate the gravitational field strength at the surface of a planet with mass 6×10²⁴kg and radius 6×10⁶m.

Solution:

$g = \frac{GM}{r^2}$

$g = \frac{6.674 \times 10^{-11} \times 6 \times 10^{24}}{(6 \times 10^6)^2}$

$g = \frac{4.0044 \times 10^{14}}{3.6 \times 10^{13}}$

$g = 11.12 \, \text{m/s}^2$

Example 4

Electric Field Due to a Point Charge

Scenario: Calculate the electric field at a point 0.5 meters away from a +2μC charge.

Solution:

$E = k_e \frac{Q}{r^2}$

$E = 8.9875 \times 10^9 \frac{2 \times 10^{-6}}{0.5^2}$

$E = 8.9875 \times 10^9 \frac{2 \times 10^{-6}}{0.25}$

$E = 8.9875 \times 10^9 \times 8 \times 10^{-6}$

$E = 71.9 \times 10^3 \, \text{N/C}$

Example 5

Comparing Gravitational and Electric Forces

Scenario: Compare the gravitational and electric forces between a proton and an electron separated by a distance of 1×10⁻¹⁰m.

Solution: Gravitational Force:

$F_g = \frac{G m_p m_e}{r^2}$

$F_g = \frac{6.674 \times 10^{-11} \times 1.67 \times 10^{-27} \times 9.11 \times 10^{-31}}{(1 \times 10^{-10})^2}$

$F_g = \frac{1.0038 \times 10^{-66}}{1 \times 10^{-20}}$

$F_g = 1.0038 \times 10^{-46} \, \text{N}$

Electric Force:

$F_e = k_e \frac{|q_1 q_2|}{r^2}$

$F_e = 8.9875 \times 10^9 \frac{(1.6 \times 10^{-19})^2}{(1 \times 10^{-10})^2}$

$F_e = 8.9875 \times 10^9 \frac{2.56 \times 10^{-38}}{1 \times 10^{-20}}$

$F_e = 2.3 \times 10^{-18} \, \text{N}$

The electric force is vastly stronger than the gravitational force between a proton and an electron.

Practice Problems

Question 1

Two masses, m₁ = 5kg and m₂ = 10kg, are placed 2 meters apart. What is the gravitational force between them? (Use G=6.674×10⁻¹¹Nm²/kg²).

A) 1.67×10⁻⁹N
B) 8.34×10⁻¹⁰N
C) 3.34×10⁻¹⁰N
D) 6.67×10⁻¹¹N

Answer: B) 8.34×10−10N

Explanation:

The gravitational force F between two masses is given by Newton’s law of gravitation:

$F = G \frac{m_1 m_2}{r^2}$

where:

G = 6.674×10⁻¹¹Nm²/kg²
m₁ = 5kg
m₂ = 10kg
r = 2m

Plug in the values:

$F = \frac{6.674 \times 10^{-11} \times 5 \times 10}{2^2}$

$F = \frac{6.674 \times 10^{-11} \times 50}{4}$

$F = \frac{333.7 \times 10^{-11}}{4}$

$F = 8.34 \times 10^{-10} \, \text{N}$

Thus, the correct answer is 8.34×10⁻¹⁰N.

Question 2

An electron and a proton are separated by a distance of 1 meter. What is the magnitude of the electrostatic force between them? (Use k = 8.99×109Nm²/C² and e = 1.6×10⁻¹⁹C).

A) 2.30×10⁻²⁸N
B) 2.30×10⁻²⁰N
C) 1.15×10⁻²⁸N
D) 1.15×10⁻¹⁰N

Answer: B) 2.30×10⁻²⁰N

Explanation:

The electrostatic force F between two charges is given by Coulomb’s law:

$F = \frac{k q_1 q_2}{r^2}$

where:

$k = 8.99 \times 10^9 \, \text{Nm}^2/\text{C}^2$

$q_1 = q_2 = e = 1.6 \times 10^{-19} \, \text{C}$

$r = 1 \, \text{m}$

Plug in the values:

$F = \frac{8.99 \times 10^9 \times (1.6 \times 10^{-19})^2}{1^2}$

$F = \frac{8.99 \times 10^9 \times 2.56 \times 10^{-38}}{1}$

$F = 2.30 \times 10^{-20} \, \text{N}$

Thus, the correct answer is 2.30×10⁻²⁰N.

Question 3

Which of the following statements correctly describes a key difference between gravitational and electromagnetic forces?

A) Gravitational force can be either attractive or repulsive, while electromagnetic force is always attractive.
B) Gravitational force acts only on masses, while electromagnetic force acts only on charges.
C) Gravitational force is much stronger than electromagnetic force.
D) Gravitational force is always attractive, while electromagnetic force can be either attractive or repulsive.

Answer: D) Gravitational force is always attractive, while electromagnetic force can be either attractive or repulsive.

Explanation:

The gravitational force is always attractive, meaning it always pulls masses toward each other. It acts on any objects with mass. On the other hand, the electromagnetic force can be either attractive or repulsive depending on the charges involved; like charges repel each other, while opposite charges attract each other. This fundamental difference is crucial in distinguishing between the two forces.

Thus, the correct answer is that gravitational force is always attractive, while electromagnetic force can be either attractive or repulsive.