Thermodynamics and Forces

Team English - Examples.com
Last Updated: September 24, 2024

Understanding the principles of thermodynamics and forces is crucial for mastering the topics related to energy, heat, work, and motion in the AP Physics exam. This section will cover the essential concepts of thermodynamics, including the laws of thermodynamics, and the interplay between thermodynamics and mechanical forces. Below are detailed notes along with five examples to help you achieve a high score on your AP Physics exam.

Free AP Physics 2: Algebra-Based Practice Test

Learning Objectives

You should understand the laws of thermodynamics, including energy conservation, entropy, and heat transfer processes. Be able to analyze and solve problems involving thermodynamic systems, heat engines, and refrigerators. For forces, grasp Newton’s laws of motion, the concepts of force, mass, and acceleration, and their application in various contexts. Master topics like gravitational, frictional, and centripetal forces, and use free-body diagrams to solve related problems efficiently.

Key Concepts in Thermodynamics

Laws of Thermodynamics

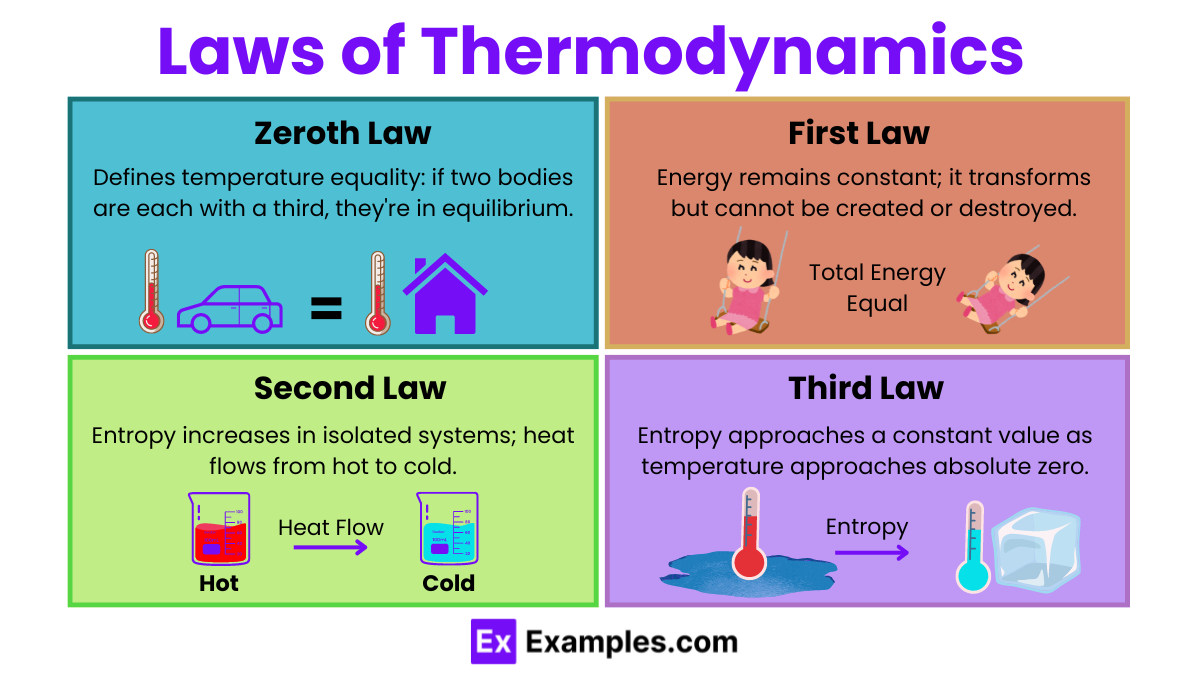
The Laws of Thermodynamics
  1. Zeroth Law of Thermodynamics:
    • If two systems are each in thermal equilibrium with a third system, then they are in thermal equilibrium with each other.
    • This law establishes the concept of temperature.
  2. First Law of Thermodynamics (Law of Energy Conservation):
    • The change in internal energy of a system is equal to the heat added to the system minus the work done by the system.
    • ΔU=Q−W
    • ΔU is the change in internal energy, Q is the heat added to the system, and W is the work done by the system.
  3. Second Law of Thermodynamics:
    • Heat cannot spontaneously flow from a colder body to a hotter body.
    • The total entropy of an isolated system can never decrease over time.
  4. Third Law of Thermodynamics:
    • As the temperature of a system approaches absolute zero, the entropy of the system approaches a constant minimum.

Concepts of Heat and Work

  • Heat (Q): Energy transferred due to a temperature difference between two objects.
  • Work (W): Energy transfer that occurs when an object is moved by a force.

Thermodynamic Processes

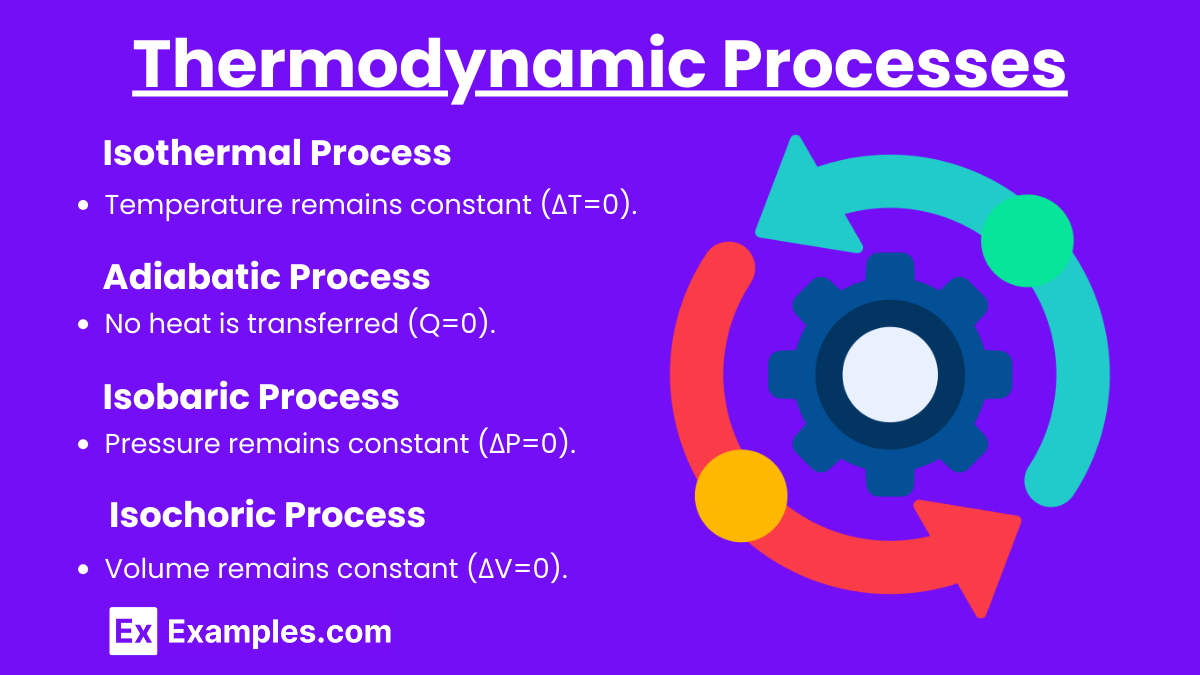
Thermodynamic Processes
  1. Isothermal Process:
    • Occurs at a constant temperature.
    • ΔU=0 .
  2. Adiabatic Process:
    • No heat is exchanged with the surroundings.
    • Q = 0, so ΔU = −W.
  3. Isobaric Process:
    • Occurs at a constant pressure.
    • Work done by the system: W = PΔV.
  4. Isochoric Process:
    • Occurs at a constant volume.
    • W = 0, so ΔU = Q.

Internal Energy

  • Internal Energy (U): The total energy contained within a system.
  • Relationship to Temperature: For an ideal gas, internal energy is directly proportional to its temperature.

Types of Forces

Types of Forces
  1. Gravitational Force:
    • Attractive force between two masses.
  2. Normal Force:
    • Perpendicular force exerted by a surface on an object in contact with it.
  3. Frictional Force:
    • Force that opposes the relative motion between two surfaces.
    • Static Friction: fₛ ≤ μₛFₙ
    • Kinetic Friction: fₖ = μₖFₙ​.
  4. Tension Force:
    • Force transmitted through a string, rope, or cable.
  5. Spring Force:
    • Force exerted by a compressed or stretched spring.
    • Hooke’s Law: Fₛ = −kx.

Newton’s Laws of Motion

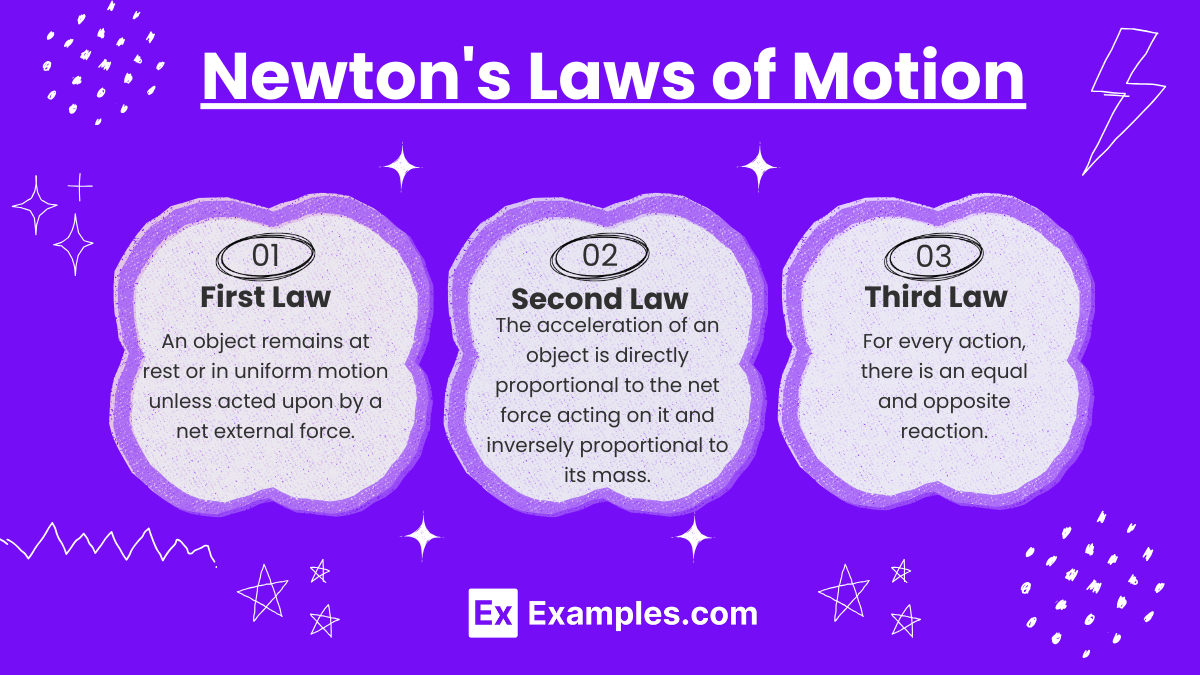
Newton's Laws of Motion
  1. First Law (Inertia):
    • An object remains at rest or in uniform motion unless acted upon by a net external force.
  2. Second Law (F = ma):
    • The acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass.
  3. Third Law (Action-Reaction):
    • For every action, there is an equal and opposite reaction.

Examples

Example 1: Isothermal Expansion of an Ideal Gas

Scenario: An ideal gas expands isothermally from a volume of 1.0m³ to 2.0m³ at a constant temperature of 300K. Calculate the work done by the gas if it is initially at a pressure of 100kPa.

Solution:

    \[ W = nRT \ln \left( \frac{V_f}{V_i} \right) \]

    \[\text{Given } P_i V_i = nRT, \text{ we can find } nRT: \]

    \[100 \, \text{kPa} \times 1.0 \, \text{m}^3 = 100 \, \text{kJ} \]

    \[W = 100 \, \text{kJ} \ln \left( \frac{2.0 \, \text{m}^3}{1.0 \, \text{m}^3} \right) \]

    \[W = 100 \, \text{kJ} \ln (2) \approx 69.3 \, \text{kJ} \]

Example 2: Adiabatic Compression of an Ideal Gas

Scenario: An ideal gas is compressed adiabatically, reducing its volume from 2.0m³ to 1.0m³. If the initial pressure and temperature are 100kPa and 300K, respectively, calculate the final temperature.

Solution:

    \[ \text{For adiabatic processes: } PV^\gamma = \text{constant and } TV^{\gamma - 1} = \text{constant} \]

    \[ T_f = T_i \left( \frac{V_i}{V_f} \right)^{\gamma - 1} \]

    \[\text{For a diatomic gas, } \gamma = 1.4: \]

    \[T_f = 300 \, \text{K} \left( \frac{2.0 \, \text{m}^3}{1.0 \, \text{m}^3} \right)^{0.4} \approx 379 \, \text{K} \]

Example 3: Work Done by a Gas in an Isobaric Process

Scenario: A gas expands isobarically at a pressure of 150kPa, increasing its volume by 0.5m³. Calculate the work done by the gas.

Solution: W = PΔV
W = 150kPa×0.5m³ = 75kJ

Example 4: Heat Transfer in an Isochoric Process

Scenario: A gas is heated in an isochoric process, raising its temperature from 200K to 400K. The gas has a heat capacity at constant volume Cᵥ ​= 20J/K. Calculate the heat added to the gas.

Solution: Q = nCᵥ​ΔT
Q = 20J/K×(400K−200K) = 4000J

Example 5: Newton’s Second Law Applied to a Block on an Incline

Scenario: A 10 kg block slides down a frictionless incline at an angle of 30⁰. Calculate the acceleration of the block.

Solution: F = ma
The component of gravitational force acting down the incline is:
Fg​ = mgsinθ
Fg​ = 10kg×9.8m/s²×sin30⁰ = 49N

    \[ a = \frac{F_g}{m} = \frac{49\, \text{N}}{10\, \text{kg}} = 4.9\, \text{m/s}^2 \]

Practice Problems

Question 1:

A gas undergoes an isothermal expansion, doing 500 J of work on its surroundings. What is the change in internal energy of the gas?

A) 0 J
B) 250 J
C) 500 J
D) -500 J

Answer: A) 0 J

Explanation:

In an isothermal process, the temperature of the gas remains constant. According to the first law of thermodynamics:

ΔU=Q−W

where ΔU is the change in internal energy, Q is the heat added to the system, and W is the work done by the system. For an isothermal process, the internal energy change ΔU is zero because the internal energy of an ideal gas depends only on temperature, which remains constant in an isothermal process.

Thus, regardless of the work done, the change in internal energy is 0 J.

Question 2:

A 10 kg object is subjected to a net force of 40 N. What is the acceleration of the object?

A) 2 m/s²
B) 4 m/s²
C) 6 m/s²
D) 8 m/s²

Answer: B) 4 m/s²

Explanation:

According to Newton’s second law of motion:

F = ma

where F is the net force, m is the mass of the object, and a is the acceleration. We can solve for acceleration a by rearranging the equation:

a = mF​

Given:

  • F = 40N
  • m = 10kg

Calculate the acceleration:

    \[ a = \frac{40 \, \text{N}}{10 \, \text{kg}} = 4 \, \text{m/s}^2 \]

Thus, the correct answer is 4 m/s².

Question 3:

A heat engine operates between a high-temperature reservoir at 600 K and a low-temperature reservoir at 300 K. What is the maximum theoretical efficiency of the engine?

A) 25%
B) 50%
C) 75%
D) 100%

Answer: B) 50%

Explanation:

The maximum theoretical efficiency η of a heat engine is given by the Carnot efficiency formula:

    \[ \eta = 1 - \frac{T_C}{T_H} \]

where T꜀​ is the absolute temperature of the cold reservoir and Tₕ​ is the absolute temperature of the hot reservoir.

Given:

  • Tₕ = 600K
  • T꜀​ = 300K

Calculate the efficiency:

    \[ \eta = 1 - \frac{300 \, \text{K}}{600 \, \text{K}} = 1 - 0.5 = 0.5 \]

Convert the efficiency to a percentage:

η =0.5×100% = 50%

Thus, the correct answer is 50%.