Images from Lenses and Mirrors
Understanding images formed by lenses and mirrors is essential in optics, a key area in AP Physics. This topic explores how light interacts with different surfaces and materials to create images. By studying the principles of reflection and refraction, and using ray diagrams, students can predict image characteristics like size, orientation, and position. Mastery of lens and mirror equations allows for solving complex problems, essential for success in both theoretical and practical applications in physics.
Learning Objectives
Learn the principles of reflection and refraction, how lenses and mirrors form images, and the differences between real and virtual images. Master the use of ray diagrams to predict image characteristics such as size, orientation, and position. Be proficient in applying mirror and lens equations to solve related problems. Additionally, understand the practical applications of these principles in optical devices like cameras, telescopes, and eyeglasses.
Reflection and Refraction
Reflection: The bouncing back of light when it hits a surface.
- Law of Reflection: The angle of incidence (θi) equals the angle of reflection (θr).
Refraction: The bending of light as it passes from one medium to another.
- Snell’s Law: n₁sin(θ₁)=n₂sin(θ₂)
- Where n₁ and n₂ are the refractive indices of the respective media, and
- θ₁ and θ₁ are the angles of incidence and refraction.
Mirrors
Types of Mirrors:
- Plane Mirrors: Flat surfaces that produce virtual, upright, and same-size images.
- Spherical Mirrors:
- Concave Mirrors: Converging mirrors that can produce real or virtual images.
- Convex Mirrors: Diverging mirrors that always produce virtual, upright, and reduced images.
Mirror Equation and Magnification:
- Mirror Equation: \[ \frac{1}{f} = \frac{1}{d_o} + \frac{1}{d_i} \]
- f: Focal length, do: Object distance, di: Image distance
- Magnification: \[ m = \frac{h_i}{h_o} = -\frac{d_i}{d_o} \]
- hi: Image height, ho: Object height
Lenses
Types of Lenses:
- Convex Lenses: Converging lenses that can produce real or virtual images.
- Concave Lenses: Diverging lenses that always produce virtual, upright, and reduced images.
Lens Equation and Magnification:
- Lens Equation: \[ \frac{1}{f} = \frac{1}{d_o} + \frac{1}{d_i} \]
- Magnification: \[ m = \frac{h_i}{h_o} = \frac{d_i}{d_o} \]
Ray Diagrams
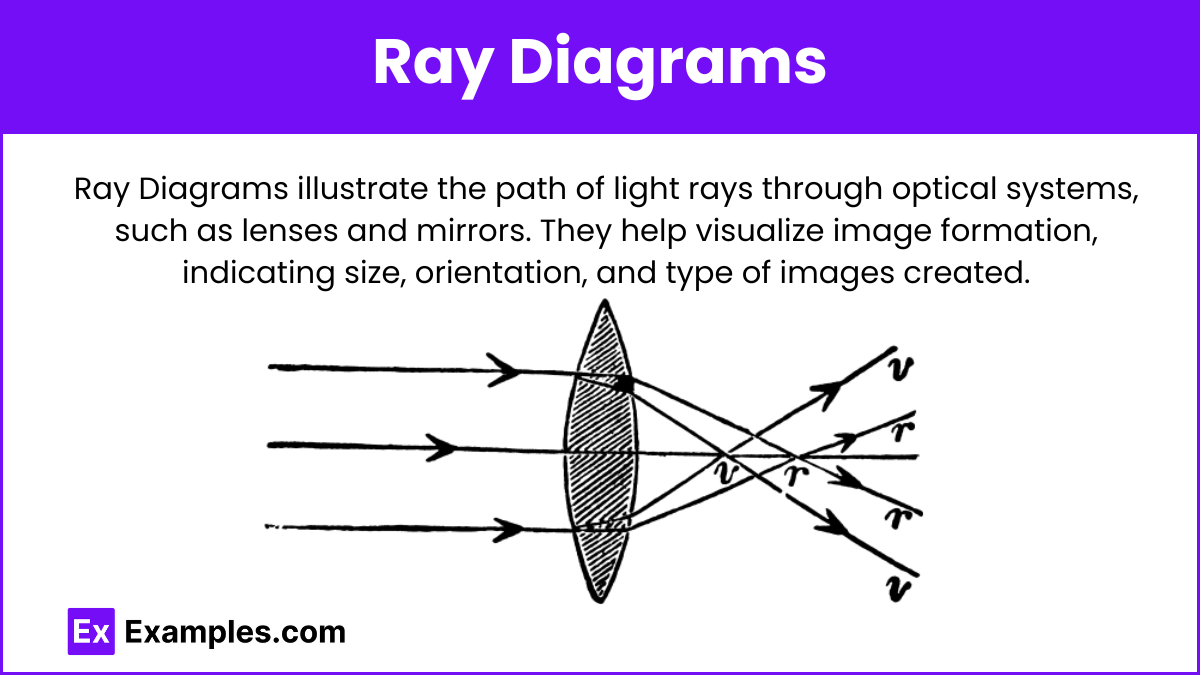
Drawing Ray Diagrams for Mirrors and Lenses:
- Concave Mirror:
- Ray parallel to the principal axis reflects through the focal point.
- Ray through the focal point reflects parallel to the principal axis.
- Ray through the center of curvature reflects back on itself.
- Convex Mirror:
- Ray parallel to the principal axis appears to diverge from the focal point.
- Ray aimed at the focal point reflects parallel to the principal axis.
- Ray aimed at the center of curvature reflects back on itself.
- Convex Lens:
- Ray parallel to the principal axis refracts through the focal point.
- Ray through the center of the lens continues straight.
- Ray through the focal point refracts parallel to the principal axis.
- Concave Lens:
- Ray parallel to the principal axis diverges as if from the focal point.
- Ray through the center of the lens continues straight.
- Ray aimed at the focal point refracts parallel to the principal axis.
Image Formation
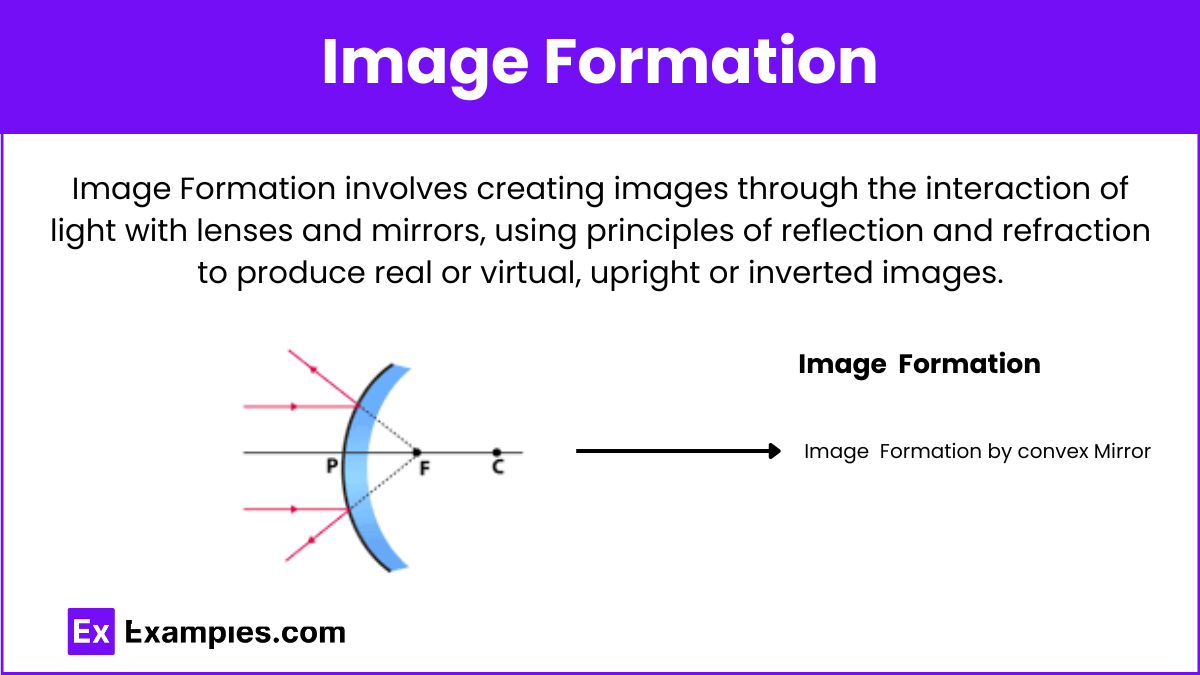
Image Characteristics:
- Real Image: Formed when light rays converge, inverted, and can be projected on a screen.
- Virtual Image: Formed when light rays appear to diverge from a point, upright, and cannot be projected on a screen.
Image Formation with Mirrors and Lenses:
- Concave Mirror and Convex Lens:
- Object beyond 2F: Image between F and 2F, real, inverted, and reduced.
- Object at 2F: Image at 2F, real, inverted, and same size.
- Object between F and 2F: Image beyond 2F, real, inverted, and enlarged.
- Object at F: No image formed (rays parallel).
- Object inside F: Image behind mirror/lens, virtual, upright, and enlarged.
- Convex Mirror and Concave Lens:
- Object position does not change image characteristics: Image always virtual, upright, and reduced.
Examples of Images from Lenses and Mirrors
- Concave Mirror:
- Shaving mirrors create enlarged, upright images when held close to the face.
- Convex Mirror:
- Rearview mirrors in vehicles provide a wide field of view with reduced, upright images.
- Convex Lens:
- Magnifying glasses produce enlarged, virtual images when objects are placed within the focal length.
- Concave Lens:
- Eyeglasses for nearsightedness use concave lenses to create virtual, upright, and reduced images.
- Plane Mirror:
- Bathroom mirrors reflect virtual, upright, and same-size images of the viewer.
Practice Test Questions on Images from Lenses and Mirrors
1. What type of image is formed by a convex mirror?
A. Real and inverted
B. Real and upright
C. Virtual and inverted
D. Virtual and upright
Answer: D. Virtual and upright
Explanation: Convex mirrors always produce virtual images because the reflected rays diverge. These images appear upright and are reduced in size, making convex mirrors useful for wide-angle views, such as in vehicle rearview mirrors.
2. When an object is placed between the focal point and a concave lens, the image formed is:
A. Real, inverted, and enlarged
B. Virtual, upright, and reduced
C. Real, upright, and reduced
D. Virtual, inverted, and enlarged
Answer: B. Virtual, upright, and reduced
Explanation: A concave lens always produces virtual images regardless of the object’s position. These images are upright and smaller than the actual object, which is why concave lenses are used in devices like eyeglasses for correcting nearsightedness.
3. If an object is placed at the focal point of a convex lens, what will be the nature of the image formed?
A. Real and at infinity
B. Virtual and at infinity
C. Real and at the focal point
D. No image is formed
Answer: A. Real and at infinity
Explanation: When an object is placed at the focal point of a convex lens, the refracted rays become parallel and do not converge to form an image at any finite distance. Therefore, the image is formed at infinity and is real. This principle is used in applications like telescopes and collimators.