Periodic Waves

Periodic waves are fundamental in understanding wave behavior and properties. In AP Physics, you study transverse and longitudinal waves, focusing on their characteristics such as amplitude, wavelength, frequency, and speed. Periodic waves repeat at regular intervals and are essential in explaining phenomena like sound and light. Mastering the wave equation, superposition principle, and standing waves is crucial for solving problems and applying these concepts in real-world contexts, ensuring a solid foundation for the AP Physics exam.

Learning Objectives

Understand the properties and types of periodic waves, including transverse and longitudinal waves. Learn how to calculate wave parameters such as frequency, period, wavelength, and wave speed. Grasp the wave equation and the principles of wave energy, superposition, and interference. Study standing waves, harmonics, and overtones. Apply these concepts to practical examples like sound and light waves, ensuring you can solve related problems accurately.

Periodic Waves

Periodic waves are waves that repeat at regular intervals. They can be categorized into two main types: transverse and longitudinal waves.

Types of Periodic Waves

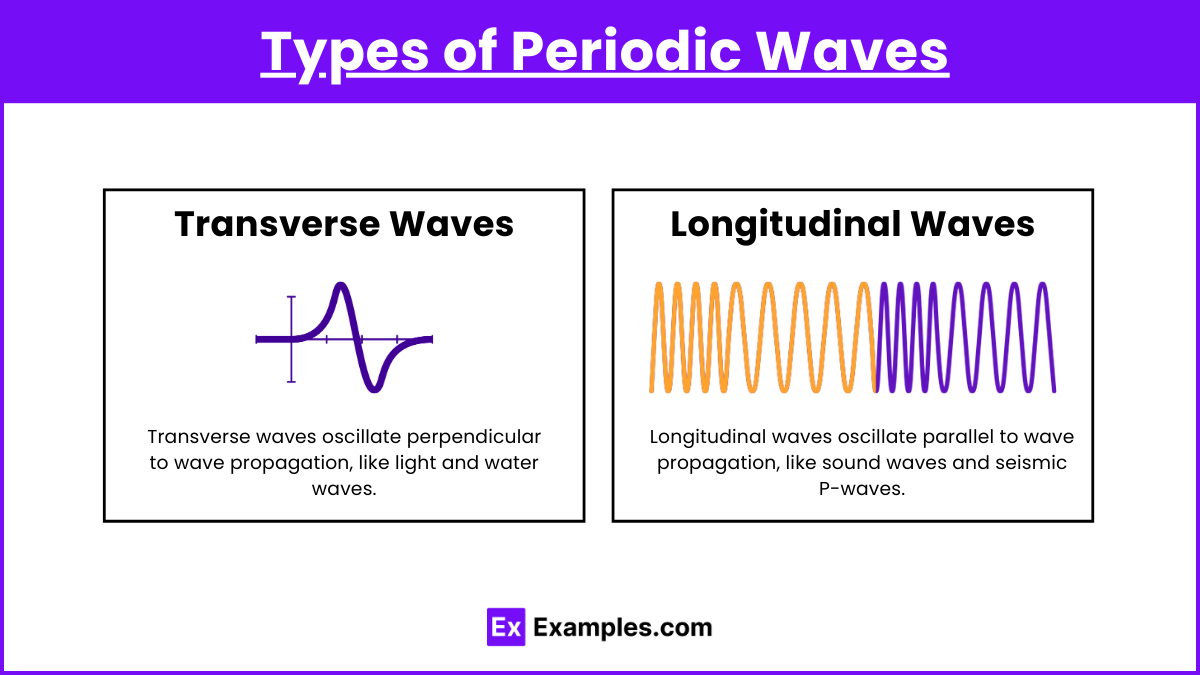
1. Transverse Waves
   • Definition: In transverse waves, the oscillation or displacement of the medium is perpendicular to the direction of wave propagation.
   • Examples: Light waves, water waves, and waves on a string.
   • Key Characteristics:
     • Crest: The highest point of the wave.
     • Trough: The lowest point of the wave.
     • Amplitude: The maximum displacement from the equilibrium position.
     • Wavelength (λ): The distance between two successive crests or troughs.
2. Longitudinal Waves
   • Definition: In longitudinal waves, the oscillation or displacement of the medium is parallel to the direction of wave propagation.
   • Examples: Sound waves, seismic P-waves.
   • Key Characteristics:
     • Compression: The region where particles are closest together.
     • Rarefaction: The region where particles are furthest apart.
     • Amplitude: The maximum displacement from the equilibrium position.
     • Wavelength (λ): The distance between two successive compressions or rarefactions.

Wave Parameters

1. Frequency (f)
   • Definition: The number of wave cycles that pass a given point per unit time.
   • Unit: Hertz (Hz)
   • Formula: f=1/T​, where T is the period.
2. Period (T)
   • Definition: The time it takes for one complete wave cycle to pass a given point.
   • Unit: Seconds (s)
   • Formula: T=1/f
3. Wave Speed (v)
   • Definition: The speed at which the wave propagates through the medium.
   • Unit: Meters per second (m/s)
   • Formula: v=fv

Wave Equations

The general form of a wave equation for a periodic wave can be expressed as:

\[ y(x, t) = A \sin(kx – \omega t + \phi) \]

• y(x,t): Displacement as a function of position (x) and time (t).
• A: Amplitude.
• k: Wave number, given by k=2π/λ.
• ω\omegaω: Angular frequency, given by ω=2πf.
• ϕ: Phase constant, determining the wave’s initial position.

Energy in Waves

• Kinetic Energy: Energy due to the motion of particles in the medium.
• Potential Energy: Energy stored due to the displacement of particles from their equilibrium position.
• Total Energy: Sum of kinetic and potential energy.

Superposition Principle

When two or more waves overlap, the resultant displacement is the sum of the individual displacements. This principle leads to interference patterns.

• Constructive Interference: Occurs when waves are in phase and their amplitudes add up.
• Destructive Interference: Occurs when waves are out of phase and their amplitudes cancel out.

Standing Waves

• Definition: Waves that remain in a constant position, characterized by nodes and antinodes.
• Nodes: Points of zero displacement.
• Antinodes: Points of maximum displacement.
• Formation: Standing waves form when two waves of the same frequency and amplitude travel in opposite directions and interfere.

Harmonics and Overtones

• Fundamental Frequency (First Harmonic): The lowest frequency of a standing wave.
• Overtones: Higher frequencies at which standing waves can form, multiples of the fundamental frequency.

Practical Applications

• Sound Waves: Used in musical instruments, medical imaging (ultrasound), and communication.
• Light Waves: Used in optics, fiber-optic communication, and various imaging technologies.

Examples of Periodic Waves

1. Sound Waves
   • Longitudinal waves where particles oscillate parallel to wave propagation, crucial in communication, music, and various technologies.
2. Light Waves
   • Transverse electromagnetic waves that travel through a vacuum, essential for vision, photography, and fiber-optic communication.
3. Water Waves
   • Transverse waves on the surface of water, caused by wind, providing insight into wave dynamics and energy transfer.
4. Seismic Waves
   • Waves traveling through Earth’s layers, used in studying earthquakes and the Earth’s internal structure, including P-waves and S-waves.
5. Electromagnetic Waves
   • Waves like radio, microwaves, and X-rays, which do not require a medium, crucial in wireless communication and medical imaging.

Practice Test Questions Of Periodic Waves

Question 1:

Which of the following is true for all periodic waves?

A) They can only travel through a vacuum.
B) They have a constant frequency and wavelength.
C) Their amplitude remains constant over time.
D) They can only be transverse waves.

Answer: B) They have a constant frequency and wavelength.

Explanation: Periodic waves are characterized by their regular, repeating pattern, meaning their frequency (the number of cycles per second) and wavelength (the distance between successive wave peaks) remain constant. This regularity is what makes them periodic.

Question 2:

What happens when two periodic waves of the same frequency and amplitude meet in phase?

A) They cancel each other out completely.
B) They form a wave with double the amplitude.
C) They continue unaffected by each other.
D) They decrease in frequency.

Answer: B) They form a wave with double the amplitude.

Explanation: When two waves meet in phase, their crests and troughs align perfectly. According to the superposition principle, the resultant wave’s amplitude is the sum of the individual amplitudes, resulting in a wave with double the amplitude.

Question 3:

Which parameter of a periodic wave is directly related to its energy?

A) Wavelength
B) Frequency
C) Amplitude
D) Speed

Answer: C) Amplitude

Explanation: The energy of a wave is proportional to the square of its amplitude. Higher amplitude means the wave carries more energy, which is why amplitude is a key indicator of the energy of a periodic wave.