Magnetic Permeability and Magnetic Dipole Moment
Understanding magnetic permeability and magnetic dipole moment is essential for mastering magnetism in AP Physics. Magnetic permeability measures a material’s ability to support a magnetic field, influencing applications like transformers and electromagnets. The magnetic dipole moment represents the strength and direction of a magnetic source, crucial for explaining the behavior of magnets and compasses. Grasping these concepts will enhance your problem-solving skills and comprehension of magnetic phenomena for the AP Physics exam.
Learning Objectives
focus on understanding the definitions and formulas of magnetic permeability and magnetic dipole moment. Learn how to calculate and apply these concepts to various materials and magnetic fields. Recognize the differences in permeability among diamagnetic, paramagnetic, and ferromagnetic materials. Understand the effects of magnetic dipole moments in external magnetic fields, including torque and potential energy. Grasp the practical applications in electromagnets, transformers, and MRI machines.
Magnetic Permeability
Magnetic permeability (μ) is a measure of how easily a material can support the formation of a magnetic field within itself. It is defined as the ratio of the magnetic flux density (B) to the magnetic field strength (H) in a given material.
\[ \mu = \frac{B}{H} \]
Types of Magnetic Permeability
- Absolute Permeability (μ): This is the permeability of a material in its pure form.
- Relative Permeability (μᵣ): This is the ratio of the permeability of a material to the permeability of free space (μ0).
\[ \mu_r = \frac{\mu}{\mu_0} \]
Permeability of Free Space (μ0)
The permeability of free space (also known as the vacuum permeability) is a physical constant denoted by μ0\mu_0μ0.
\[ \mu_0 = 4\pi \times 10^{-7} \, \text{H/m} \]
Factors Affecting Magnetic Permeability
- Material Composition: Different materials have different permeabilities.
- Temperature: Permeability can change with temperature.
- Frequency of the Applied Magnetic Field: Permeability can vary with the frequency of the applied magnetic field.
Magnetic Permeability of Various Materials
- Diamagnetic Materials: μr<1(e.g., bismuth, copper)
- Paramagnetic Materials: μr≈1(e.g., aluminum, platinum)
- Ferromagnetic Materials: μr>1(e.g., iron, nickel)
Applications of Magnetic Permeability
- Electromagnets: Designing electromagnets with high permeability materials to enhance magnetic field strength.
- Transformers: Using materials with high permeability to improve the efficiency of transformers.
- Magnetic Shielding: Employing materials with specific permeability to shield sensitive equipment from external magnetic fields.
Magnetic Dipole Moment
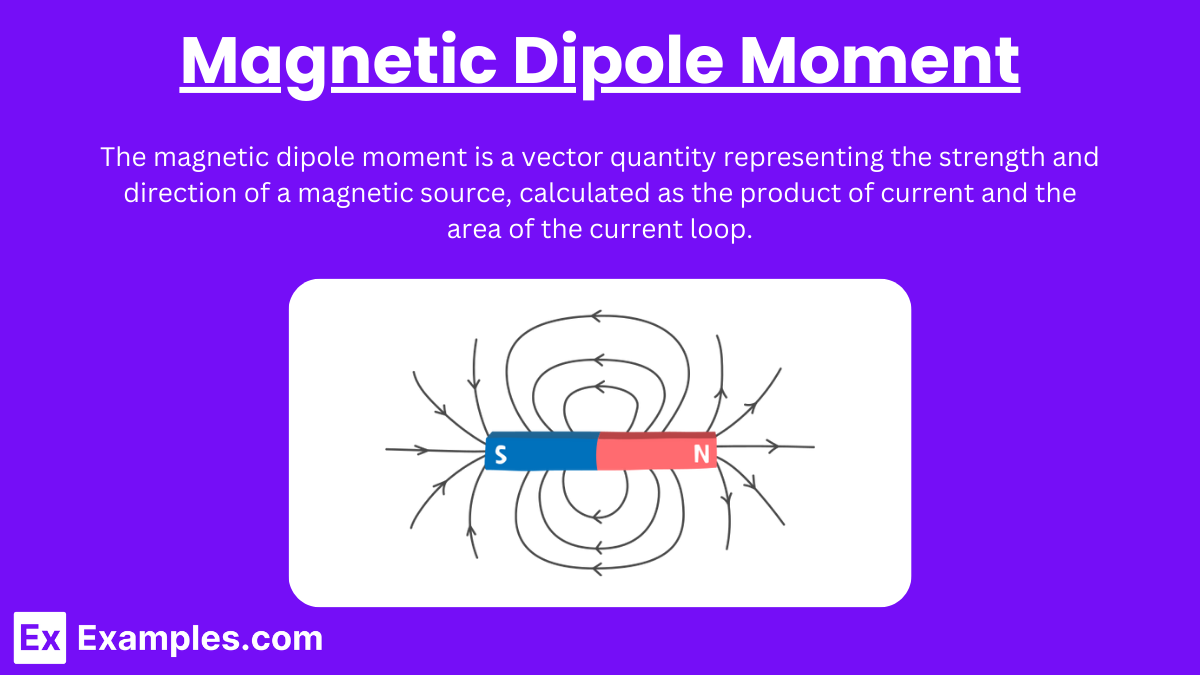
The magnetic dipole moment (μ) is a vector quantity that represents the strength and direction of a magnetic source. It is analogous to the electric dipole moment in electrostatics.
Formula
For a current loop of area A carrying current III, the magnetic dipole moment is given by:
μ=I⋅A
Direction
The direction of the magnetic dipole moment is given by the right-hand rule: if the fingers of the right hand curl in the direction of the current, the thumb points in the direction of the magnetic dipole moment.
Magnetic Dipole in a Magnetic Field
When a magnetic dipole is placed in a magnetic field (B), it experiences a torque (τ) given by:
τ=μ×B
The potential energy (U) of a magnetic dipole in a magnetic field is:
U=−μ⋅BU
Applications of Magnetic Dipole Moment
- Magnetic Materials: Understanding the magnetic properties of materials.
- Compass Needles: The Earth’s magnetic field aligns compass needles due to their magnetic dipole moments.
- MRI Machines: Magnetic resonance imaging (MRI) exploits the magnetic dipole moments of nuclei in a magnetic field for medical imaging.
Comparison of Magnetic Dipole Moment and Electric Dipole Moment
- Nature: Magnetic dipole moment is due to current loops or spin of electrons, while electric dipole moment is due to separation of positive and negative charges.
- Field Lines: Magnetic dipole fields are closed loops, while electric dipole fields originate from positive charges and end on negative charges.
Examples and Applications
- Earth’s Magnetic Field: The Earth itself acts as a giant magnet with a magnetic dipole moment.
- Bar Magnets: A simple bar magnet has a north and south pole with a magnetic dipole moment pointing from the south to the north pole.
Examples of Magnetic Permeability and Magnetic Dipole Moment
- Electromagnets: Utilizing high permeability materials to enhance magnetic field strength in devices like cranes and maglev trains.
- Transformers: Using iron cores with high magnetic permeability to improve efficiency in power transmission.
- MRI Machines: Exploiting the magnetic dipole moments of nuclei in strong magnetic fields for medical imaging.
- Compass Needles: Aligning with Earth’s magnetic field due to their magnetic dipole moments.
- Bar Magnets: Exhibiting magnetic dipole moments with distinct north and south poles affecting magnetic field lines.
Practice Test Questions on Magnetic Permeability and Magnetic Dipole Moment
1. Which of the following best describes magnetic permeability?
A. The ratio of the magnetic field strength to the magnetic flux density
B. The measure of a material’s ability to support the formation of a magnetic field within itself
C. The strength and direction of a magnetic source
D. The potential energy of a magnetic dipole in a magnetic field
Answer: B. The measure of a material’s ability to support the formation of a magnetic field within itself
Explanation: Magnetic permeability (μ) is defined as the measure of how easily a material can support the formation of a magnetic field within itself. It is given by the ratio of the magnetic flux density (B) to the magnetic field strength (H).
2. The magnetic dipole moment is calculated using which of the following formulas?
\[ \text{A. } \mu = \frac{B}{H} \]
B. τ=μ×B
C. μ=I⋅A
\[ \text{D. } \mu_r = \frac{\mu}{\mu_0} \]
Answer: C. μ=I⋅A
Explanation: The magnetic dipole moment (μ) is calculated as the product of the current (I) and the area (A) of the loop. It represents the strength and direction of a magnetic source.
3. Which type of material typically has a relative permeability (μᵣ) less than 1?
A. Ferromagnetic
B. Paramagnetic
C. Diamagnetic
D. Superparamagnetic
Answer: C. Diamagnetic
Explanation: Diamagnetic materials have a relative permeability (μᵣ) less than 1. This means they are weakly repelled by magnetic fields and do not retain any magnetization in the absence of an external magnetic field. Examples include bismuth and copper.