Square 1 to 25
Square 1 to 25
In mathematics, particularly in algebra, the concept of squaring integers from 1 to 25 forms a foundational aspect of understanding rational and irrational numbers. Squaring an integer—multiplying it by itself—produces a perfect square, which is always a rational number. These squares, ranging from 1212 to 252252, highlight the progression of numbers and their inherent patterns, crucial for applications like the least squares method in statistics. This exploration not only deepens our grasp of number theory but also illustrates the significant role of squares and square roots in various mathematical disciplines.
Download Squares 1 to 25 in PDF
Squaring a number means multiplying that number by itself. The result is called a “square.” For example, squaring the number 5 means calculating 5×5, which equals 25. Squares are fundamental in mathematics, particularly in algebra, where they help form the basis for more complex equations and functions.
Square 1 to 25
Highest Value: 25² = 625
Lowest Value: 1² = 1
Squares 1 to 25 Chart
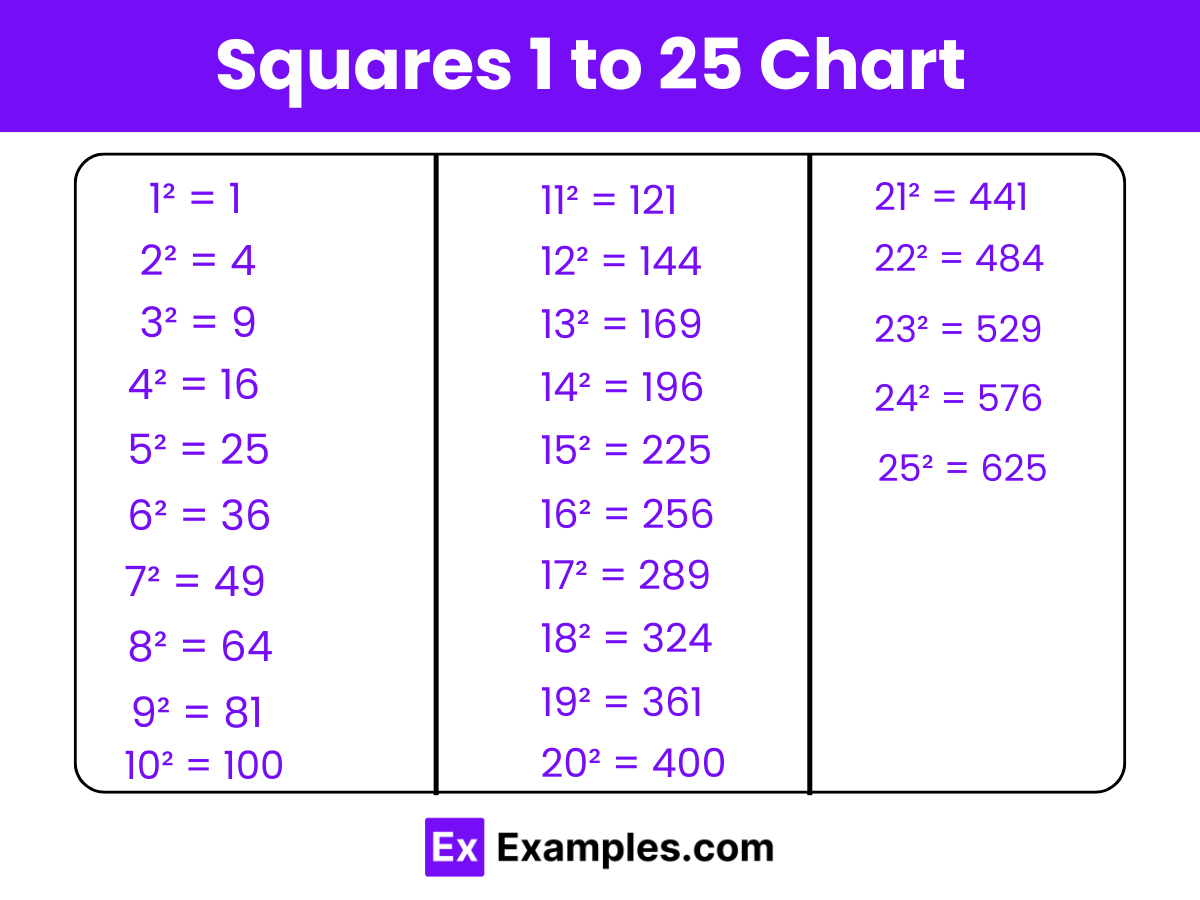
Download Squares 1 to 25 in PDF
| Squares from 1 to 25 | |
| 12 = 1 | 152 = 225 |
| 22 = 4 | 162 = 256 |
| 32 = 9 | 172 = 289 |
| 42 = 16 | 182 = 324 |
| 72 = 49 | 192 = 361 |
| 62 = 36 | 202 = 400 |
| 82 = 64 | 212 = 441 |
| 92 = 81 | 222 = 484 |
| 102 = 100 | 232 = 529 |
| 112 = 121 | 242 = 576 |
| 122 = 144 | 222 = 484 |
| 132 = 169 | 252 = 625 |
| 142 = 196 | |
The chart above lists integers from 1 to 25 alongside their squares, which are the results of multiplying each integer by itself. This representation is essential for visualizing the progression of square numbers, a fundamental concept in algebra and number theory.
More About Square of 1 to 25
Square 1 to 25 – Even Numbers
| Number | Square |
|---|---|
| 22 | 4 |
| 42 | 16 |
| 62 | 36 |
| 82 | 64 |
| 102 | 100 |
| 122 | 144 |
| 142 | 196 |
| 162 | 256 |
| 182 | 324 |
| 202 | 400 |
| 222 | 484 |
| 242 | 576 |
The chart above displays the squares of even numbers from 2 to 24, illustrating the quadratic increase as each number is multiplied by itself. This pattern emphasizes the progressive growth of square values as the base even numbers increase.
Square 1 to 25 – Odd Numbers
| Number | Square |
|---|---|
| 12 | 1 |
| 32 | 9 |
| 52 | 25 |
| 72 | 49 |
| 92 | 81 |
| 112 | 121 |
| 132 | 169 |
| 152 | 225 |
| 172 | 289 |
| 192 | 361 |
| 212 | 441 |
| 232 | 529 |
| 252 | 625 |
The table above lists the squares of odd numbers from 1 to 25. Squaring a number involves multiplying it by itself. For odd numbers, which are integers not divisible by 2, this squaring process results in a unique set of square values that show a clear pattern of increasing quadratically. As the base odd number increases, the square values rise disproportionately, illustrating the concept that the square of a larger number grows significantly faster than the number itself. This pattern is crucial for understanding mathematical concepts involving powers and growth rates.
How to Calculate the Values of Squares 1 to 25?
Understand Squaring:
- Squaring a number means multiplying that number by itself. For example, to square the number 3, you multiply 3 by 3 to get 9.
Start from 1 and Go Up to 25:
- Begin with the smallest number in the range, which is 1. Square it by multiplying it by itself: 1×1=11×1=1.
- Move to the next number, 2, and do the same: 2×2 = 4.
- Continue this process sequentially through to 25.
Use a Calculator for Efficiency:
- While you can easily square numbers manually up to 25, using a calculator can speed up the process and reduce errors, especially as the numbers get larger.
Record Your Results:
- It can be helpful to write down each result as you calculate it. Creating a table with two columns, one for the number and one for its square, can organize the information clearly.
Review the Pattern:
- Once you have all the squares calculated, review them to see the pattern of how square values increase. This can help in understanding quadratic growth and the relationship between consecutive squares.
Tricks to Remember
Use Patterns:
- Notice patterns in squares, especially for small numbers. For instance, the difference between consecutive squares (e.g., 1, 4, 9, 16) increases by 2 each time: 3, 5, 7, 9, etc.
Group and Memorize:
- Break down the list into smaller groups. For example, memorize squares 1-5 first, then 6-10, and so on. This makes the task less daunting and easier to manage.
Leverage Mnemonics:
- Create mnemonics or phrases where each word starts with a letter representing a number. For example, “Five Five’s Twenty-Five” can help you remember that 5 squared is 25.
Utilize the End Digits Rule:
- Remember patterns in the last digits of squares. For instance, squares of numbers ending in 0 end in 0 (e.g., 10² = 100), numbers ending in 1 or 9 end in 1 (e.g., 11² = 121, 19² = 361), numbers ending in 2 or 8 end in 4 (e.g., 12² = 144, 18² = 324), and so on.
Visual Aids:
- Use charts or flashcards. Visually seeing the numbers repeatedly can help solidify them in memory.
Practice with Apps:
- Use educational apps that turn learning into games, like those that quiz you on square numbers. This can make the learning process more engaging and less tedious.
Teach Someone Else:
- Explain the list of squares to someone else. Teaching is a powerful method to reinforce your own learning.
Associate with Real-Life Applications:
- Relate squares to real-life scenarios, such as areas of squares. For example, if you think of a square garden with sides of 4 meters, it helps to remember that its area (16 m²) comes from squaring the number 4.
FAQs
How does understanding squares from 1 to 25 help in learning more advanced mathematics?
Understanding these squares helps in learning more advanced topics like algebra, calculus, and statistics, where powers and roots play fundamental roles in analysis and solving problems.
What pattern do the squares of numbers from 1 to 25 follow?
The squares of numbers from 1 to 25 follow a quadratic growth pattern, where each square grows increasingly larger than the previous one at a rate that itself increases.
What is the Value of Squares 1 to 25?
The value of square 1 to 25 is the list of numbers obtained by multiplying an integer (1 – 25) by itself. It will always be a positive number. Between 1 to 25, the numbers 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24 are even numbers and 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25 are odd numbers.
How can you calculate the squares of numbers from 1 to 25?
To calculate the squares of numbers from 1 to 25, multiply each number by itself in sequence. You can use a calculator for accuracy and efficiency, especially as the numbers increase.
Why is it important to know the squares of numbers?
Knowing the squares of numbers is crucial in mathematics for solving equations, understanding geometric concepts like area, and in applications involving power and exponential growth.
Share :
