Square 1 to 30
Square 1 to 30
Exploring squares from 1 to 30 delves into fundamental principles of mathematics, including algebra and number theory. Squaring each integer illuminates the intricate relationships between rational and irrational numbers, crucial for understanding concepts like square and square roots. This sequence of squares lays the groundwork for exploring quadratic equations and serves as a cornerstone for more advanced mathematical techniques. Furthermore, it provides valuable insights into the least squares method in statistics, facilitating data analysis and modeling in various fields. Understanding these squares enhances numerical literacy and fosters a deeper appreciation for the elegance and utility of mathematical principles.
Download Squares 1 to 30 in PDF
The square of numbers from 1 to 30 refers to the result obtained by multiplying each integer in this range by itself, showcasing a fundamental mathematical operation that plays a crucial role in algebra, number theory, and various applications.
Square 1 to 30
Highest Value: 30² = 900
Lowest Value: 1² = 1
Squares 1 to 30 Chart
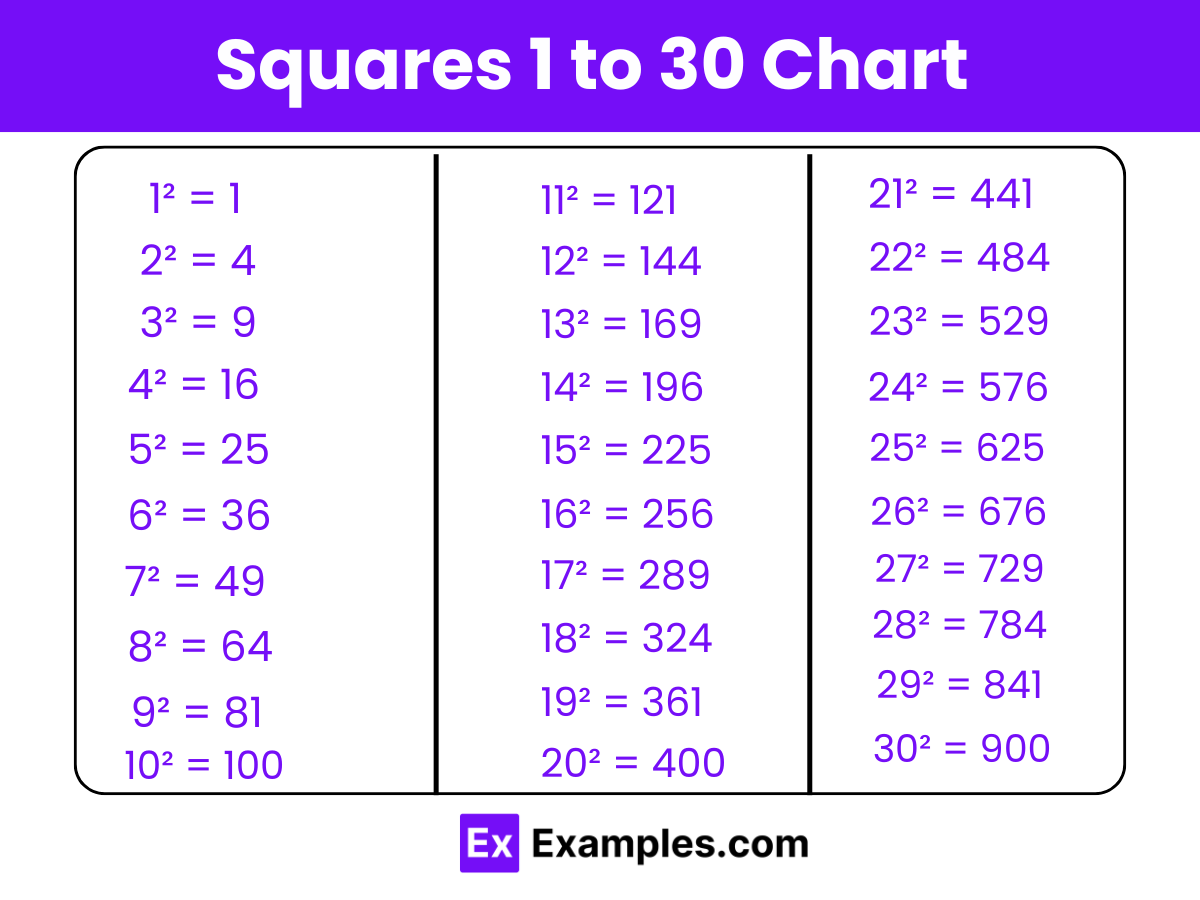
Download Squares 1 to 30 in PDF
| List of All Squares from 1 to 30 | |
| 1² = 1 | 16² = 256 |
| 2² = 4 | 17² = 289 |
| 3² = 9 | 18² = 324 |
| 4² = 16 | 19² = 361 |
| 5² = 25 | 20² = 400 |
| 6² = 36 | 21² = 441 |
| 7² = 49 | 22² = 484 |
| 8² = 64 | 23² = 529 |
| 9² = 81 | 24² = 576 |
| 10² = 100 | 25² = 625 |
| 11² = 121 | 26² = 676 |
| 12² = 144 | 27² = 729 |
| 13² = 169 | 28² = 784 |
| 14² = 196 | 29² = 841 |
| 15² = 225 | 30² = 900 |
Here, squares 1 to 30 can help students to recognize all perfect squares from 1 to 900 and approximate a square root by interpolating between known squares.
More About Square of 1 to 30
Square 1 to 30 – Even Numbers
| Number | Square |
|---|---|
| 2² | 4 |
| 4² | 16 |
| 6² | 36 |
| 8² | 64 |
| 10² | 100 |
| 12² | 144 |
| 14² | 196 |
| 16² | 256 |
| 18² | 324 |
| 20² | 400 |
| 22² | 484 |
| 24² | 576 |
| 26² | 676 |
| 28² | 784 |
| 30² | 900 |
This table displays the squares of even numbers from 2 to 30, obtained by multiplying each even integer by itself. It highlights the pattern of quadratic growth in even square values, essential in understanding mathematical relationships and applications.
Square 1 to 30 – Odd Numbers
| Number | Square |
|---|---|
| 1² | 1 |
| 3² | 9 |
| 5² | 25 |
| 7² | 49 |
| 9² | 81 |
| 11² | 121 |
| 13² | 169 |
| 15² | 225 |
| 17² | 289 |
| 19² | 361 |
| 21² | 441 |
| 23² | 529 |
| 25² | 625 |
| 27² | 729 |
| 29² | 841 |
This table presents the squares of odd numbers from 1 to 30, showcasing their quadratic growth pattern and fundamental mathematical properties.
How to Calculate the Values of Squares 1 to 30?
To calculate the squares of numbers from 1 to 30, you can follow these steps:
Understand Squaring:
- Squaring a number means multiplying it by itself. For example, squaring 3 means calculating 3×3 = 9.
Start from 1 and Go Up to 30:
- Begin with the smallest number in the range, which is 1. Square it by multiplying it by itself: 1×1 = 1.
- Move to the next number, 2, and do the same: 2×2 = 4.
- Continue this process sequentially through to 30.
Use a Calculator for Efficiency:
- While you can easily square numbers manually up to 30, using a calculator can speed up the process and reduce errors, especially as the numbers increase.
Record Your Results:
- It can be helpful to write down each result as you calculate it. Creating a table with two columns, one for the number and one for its square, can organize the information clearly.
Review the Pattern:
- Once you have all the squares calculated, review them to see the pattern of how square values increase. This can help in understanding quadratic growth and the relationship between consecutive squares.
Tricks to Remember
- Memorize the Squares of Small Numbers: Start by memorizing the squares of small numbers (1 to 10), as they are commonly used and form the foundation for larger squares.
- Identify Patterns: Notice patterns in the squares, such as the last digits or the differences between consecutive squares. For example, the last digit of squares alternates between 0, 1, 4, 9, 6, and 5.
- Use Mnemonics: Create mnemonics or memorable phrases to associate with the squares. For instance, “Three squared is nine” or “Seven squared is forty-nine”.
- Group Numbers: Group the squares into smaller sets, such as 1-5, 6-10, 11-15, and so on. Focus on memorizing one group at a time to make the task more manageable.
- Visualize Squares: Visualize the squares as geometric shapes, like a square garden with sides representing the numbers. This can help reinforce the relationship between the number and its square.
- Practice Regularly: Regular practice and repetition are key to memorization. Use flashcards, quizzes, or online resources to test yourself regularly on the squares.
- Associate with Real-Life Scenarios: Relate the squares to real-life situations, such as calculating areas or estimating quantities. For example, if a room is 10 feet by 10 feet, its area is 100 square feet.
- Teach Someone Else: Teaching the squares to someone else can reinforce your own understanding and help you remember them better.
FAQs
What patterns exist in square numbers from 1 to 30?
Square numbers exhibit a quadratic growth pattern. When plotted on a graph, they form a parabolic curve. Additionally, certain patterns emerge in the digits of square numbers, providing insights into their properties.
What is the Value of Squares 1 to 30?
The value of squares 1 to 30 is the list of numbers obtained by multiplying an integer by itself. When we multiply a number by itself we will always get a positive number. For example, the square of 12 is 132 = 169.
What are the Methods to Calculate Squares from 1 to 30?
You can calculate the squares from 1 to 30 by simply squaring each number individually (e.g., 1212 to 302302) or by using a calculator for efficiency. Additionally, recognizing patterns and employing mental math techniques can expedite the process.
How can I memorize square numbers from 1 to 30?
Memorizing the squares of numbers from 1 to 30 can be facilitated through mnemonic devices, visual aids like charts or flashcards, and practice exercises. Breaking down the list into smaller groups can also aid in memorization.
What is the relationship between square roots and square numbers?
- The square root of a number is the value that, when multiplied by itself, gives the original number. For square numbers, the square root is an integer. For instance, the square root of 16 is 4 because 4×4 = 16.
Share :
