Square 1 to 40
Square 1 to 40
Exploring squares from 1 to 40 illuminates fundamental principles of mathematics, encompassing algebraic expressions, integer properties, and the concept of rational and irrational numbers. Understanding the relationship between perfect squares and their squares and square roots is crucial in algebra and number theory, laying the groundwork for advanced mathematical concepts. This sequence of squares serves as a cornerstone for analyzing quadratic equations and applying the least square method in statistics. The study of these squares enhances numerical literacy, fostering a deeper understanding of mathematical patterns and relationships.
Download Squares 1 to 40 in PDF
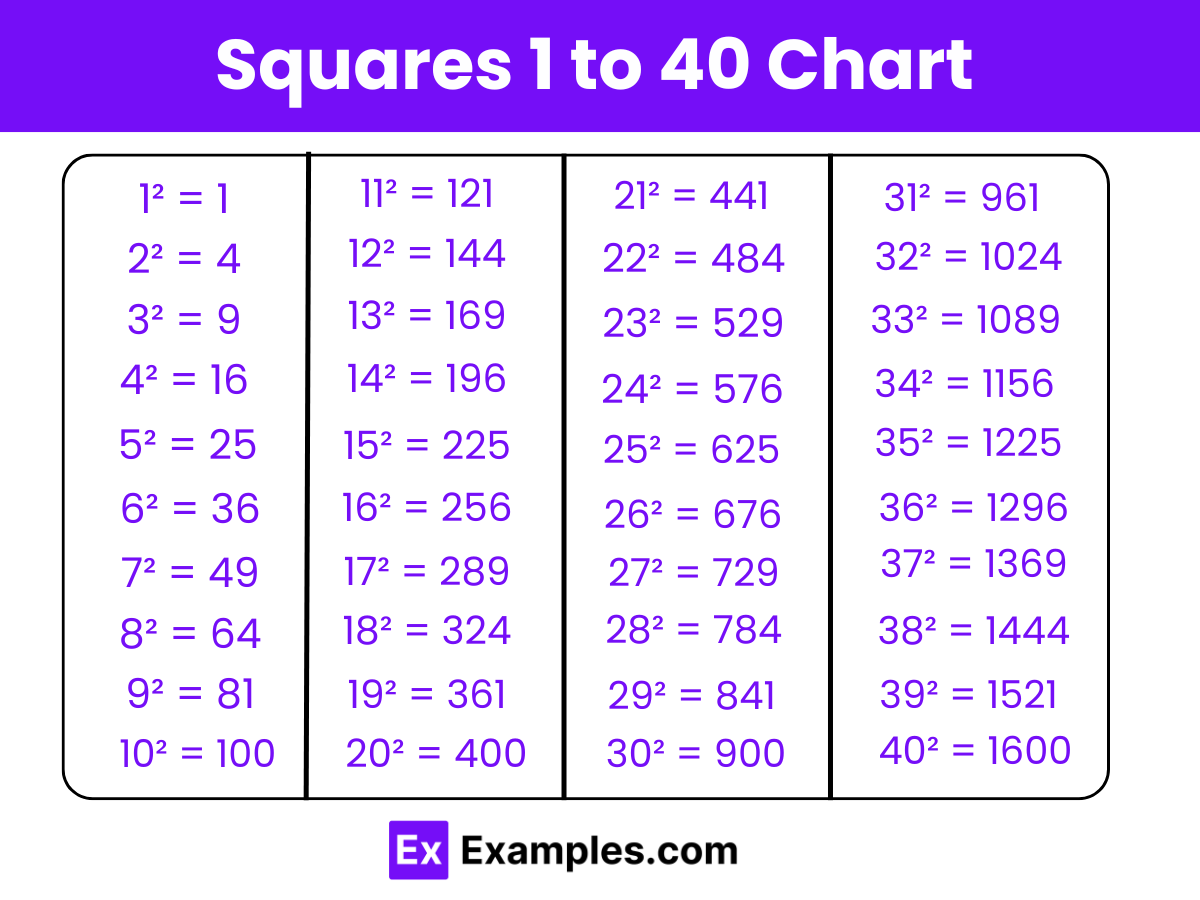
The squares from 1 to 40 represent the result of multiplying each integer in this range by itself, showcasing fundamental mathematical operations and providing insights into quadratic growth patterns. Understanding these squares is essential for various mathematical concepts, including algebra, number theory, and statistical analysis.
Square 1 to 40
Highest Value: 40² = 1600
Lowest Value: 1² = 1
Squares 1 to 40 Chart
Download Squares 1 to 40 in PDF
| List of All Squares from 1 to 40 | |
|---|---|
| 1² = 1 | 21² = 441 |
| 2² = 4 | 22² = 484 |
| 3² = 9 | 23² = 529 |
| 4² = 16 | 24² = 576 |
| 5² = 25 | 25² = 625 |
| 6² = 36 | 26² = 676 |
| 7² = 49 | 27² = 729 |
| 8² = 64 | 28² = 784 |
| 9² = 81 | 29² = 841 |
| 10² = 100 | 30² = 900 |
| 11² = 121 | 31² = 961 |
| 12² = 144 | 32² = 1024 |
| 13² = 169 | 33² = 1089 |
| 14² = 196 | 34² = 1156 |
| 15² = 225 | 35² = 1225 |
| 16² = 256 | 36² = 1296 |
| 17² = 289 | 37² = 1369 |
| 18² = 324 | 38² = 1444 |
| 19² = 361 | 39² = 1521 |
| 20² = 400 | 40² = 1600 |
This content lists the squares of numbers from 1 to 20 and their values, showcasing the result of multiplying each integer by itself. It provides a clear demonstration of the quadratic growth pattern exhibited by perfect squares, essential in mathematics and various applications.
More About Square of 1 to 40
Square 1 to 40 – Even Numbers
| 2² = 4 | 22² = 484 |
| 4² = 16 | 24² = 576 |
| 6² = 36 | 26² = 676 |
| 8² = 64 | 28² = 784 |
| 10² = 100 | 30² = 900 |
| 12² = 144 | 32² = 1024 |
| 14² = 196 | 34² = 1156 |
| 16² = 256 | 36² = 1296 |
| 18² = 324 | 38² = 1444 |
| 20² = 400 | 40² = 1600 |
This content displays the squares of even numbers from 1 to 40, highlighting the result of multiplying each even integer by itself and illustrating the quadratic growth pattern of perfect squares. It offers insight into the relationship between even numbers and their squares, fundamental in algebra and number theory.
Square 1 to 40 – Odd Numbers
| 1² = 1 | 21² = 441 |
| 3² = 9 | 23² = 529 |
| 5² = 25 | 25² = 625 |
| 7² = 49 | 27² = 729 |
| 9² = 81 | 29² = 841 |
| 11² = 121 | 31² = 961 |
| 13² = 169 | 33² = 1089 |
| 15² = 225 | 35² = 1225 |
| 17² = 289 | 37² = 1369 |
| 19² = 361 | 39² = 1521 |
This content showcases the squares of odd numbers from 1 to 40, demonstrating the result of multiplying each odd integer by itself and illustrating the quadratic growth pattern of perfect squares. It provides insight into the relationship between odd numbers and their squares, fundamental in algebra and number theory.
How to Calculate the Values of Squares 1 to 40?
To calculate the squares of numbers from 1 to 40:
- Understand Squaring: Squaring a number means multiplying it by itself.
- Start from 1 and Go Up to 40: Begin with the smallest number in the range, which is 1, and square it (1² = 1). Proceed sequentially up to 40, squaring each number along the way.
- Use Multiplication: To square a number, multiply it by itself. For example, to find the square of 5, calculate 5 × 5 = 25.
- Record Your Results: Write down the square of each number as you calculate it to keep track of your progress.
- Verify Patterns: Observe patterns in the resulting squares to enhance understanding. Notice how the square values increase as the numbers do, forming a quadratic growth pattern.
Tricks to Remember
- Learn the Squares of Small Numbers: Start by memorizing the squares of numbers from 1 to 10, as they are commonly used and form the foundation for larger squares.
- Identify Patterns: Notice patterns in the squares, such as the last digits or the differences between consecutive squares. For example, the square of an even number always ends in 4, while the square of an odd number always ends in 1.
- Use Visualizations: Visualize the square of a number as the area of a square with sides equal to that number. This mental image can help reinforce the relationship between the number and its square.
- Group Numbers: Group the squares into smaller sets, such as 1-10, 11-20, and so on. Focus on memorizing one group at a time to make the task more manageable.
- Create Mnemonics: Create mnemonics or memorable phrases to associate with the squares. For example, “Three squared is nine” or “Seven squared is forty-nine”.
- Practice Regularly: Regular practice and repetition are key to memorization. Use flashcards, quizzes, or online resources to test yourself regularly on the squares.
- Associate with Real-Life Scenarios: Relate the squares to real-life situations, such as calculating areas or estimating quantities. For example, if a room is 5 meters by 5 meters, its area is 25 square meters.
FAQs
What is the Value of Squares 1 to 40?
The squares of numbers from 1 to 40 range from 1 to 1600. They represent the result of multiplying each integer by itself, showcasing a quadratic growth pattern fundamental in mathematics.
How do you calculate the square of a number?
o calculate the square of a number, you multiply the number by itself. For example, the square of 7 is 7 × 7 = 49.
How can I remember the squares of numbers from 1 to 40?
You can use mnemonic devices, visualizations, and practice techniques to memorize the squares efficiently. Breaking the numbers into smaller groups and identifying patterns can also aid in memorization.
What are some practical uses of knowing the squares of numbers?
Understanding squares is essential in various fields such as engineering, physics, and computer science. It is used in calculations involving areas, volumes, distances, and more.
Why are some numbers called perfect squares?
Numbers that are the squares of integers are called perfect squares because they represent the area of a square with integer side lengths.
Share :
