What is the square of 30?
800
850
900
950

The Long Division method for square roots is a manual technique that provides a precise way to find the square root of any number. It identifies rational roots for perfect squares and square roots approximates irrational roots otherwise, connecting with concepts in algebra and integer operations. This method is significant for both academic learning and practical applications, including in the least squares method of regression analysis. By systematically dividing and estimating, the Long Division method unfolds the intricate relationships between numbers, revealing their mathematical properties.
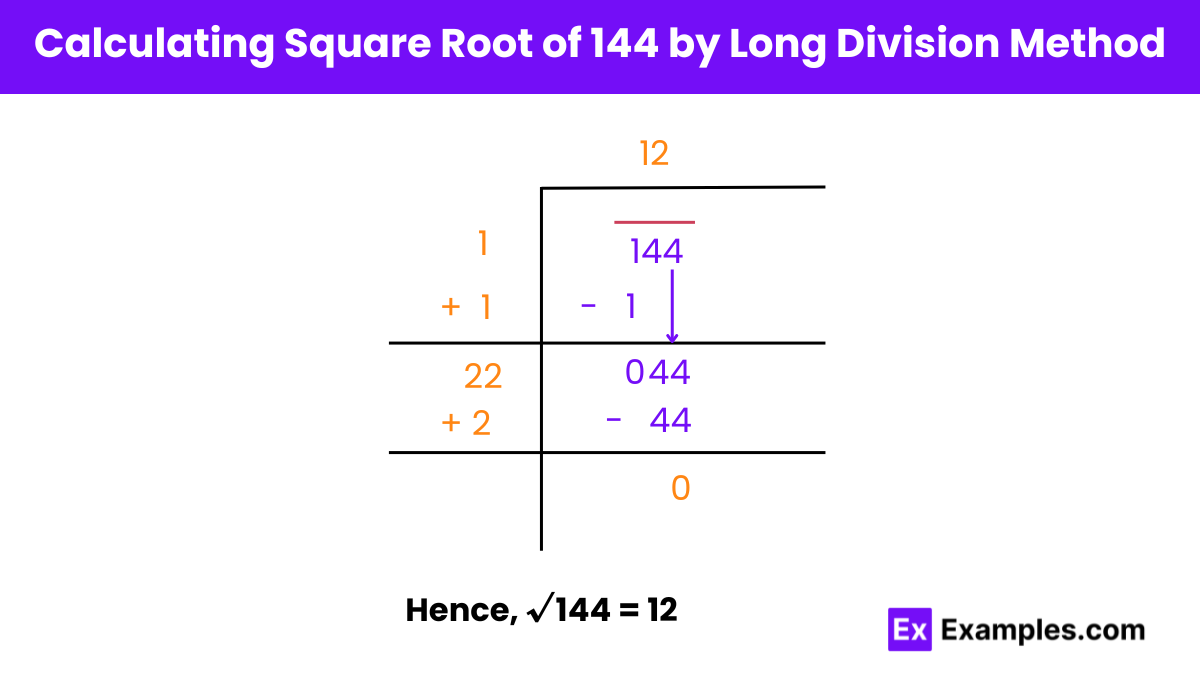
Pair the Digits: Since 144 is a three-digit number, pair the digits from the right: 1|44.
Estimate the Largest Digit: Find the largest integer whose square is less than or equal to 1 (the first pair). This is 1 because 1² = 1. Write this as the first digit of the root.
Current root: 1
Subtract 1² = 1 from 1, which gives 0.
Bring Down the Next Pair: Bring down the next pair 44 to the right of 0 to form 44.
Double the Result: Double the current result, which is 1, to get 2.
New divisor: 2
Find the Largest Digit for the Divisor: Find the largest digit (trial digit) that can be placed in the blank space of the new divisor such that the product of this number with itself and the divisor does not exceed 44.
Current root: 12
Result: The square root of 144 is 12.
Pair the Digits: Separate 529 into pairs: 5|29.
Estimate the Largest Digit: Find the largest digit whose square is less than or equal to 5. This is 2, because 2²=4.
Current root: 2
Subtract 4 from 5 to get 1.
Bring Down the Next Pair: Bring down 29 to the right of 1 to form 129.
Double the Result: Double the current result (2) to get 4.
New divisor: 4
Find the Largest Digit for the Divisor: Find the digit to fill in the blank that, when multiplied, gives a result less than or equal to 129.
Final root: 23
The square root of 529 is 23.
Pair the Digits: Separate 169 into pairs: 1|69.
Estimate the Largest Digit: The largest digit whose square is less than or equal to 1 is 1.
Current root: 1
Subtract 1² = 1 from 1 to get 0.
Bring Down the Next Pair: Bring down 69 to the right of 0 to form 69.
Double the Result: Double the current result (1) to get 2.
New divisor: 2
Find the Largest Digit for the Divisor: Find the digit that fills in the blank and produces a product less than or equal to 69.
Final root: 13
The square root of 169 is 13.
Pair the Digits: Separate 625 into pairs: 6|25.
Estimate the Largest Digit: The largest digit whose square is less than or equal to 6 is 2.
Current root: 2
Subtract 2² = 4 from 6 to get 2.
Bring Down the Next Pair: Bring down 25 to the right of 2 to form 225.
Double the Result: Double the current result (2) to get 4.
New divisor: 4
Find the Largest Digit for the Divisor: Find the digit that fills in the blank and produces a product less than or equal to 225.
Final root: 25
The square root of 625 is 25.
Not directly, as square roots of negative numbers require imaginary units. However, the same logic can apply to find the modulus of complex roots.
Yes, it can handle decimals and fractions by pairing digits to the right of the decimal point, allowing calculation of square roots for both integers and non-integer numbers.
It provides high accuracy and does not require advanced tools, making it ideal for situations where a calculator is unavailable and precise square root calculations are needed.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the square of 30?
800
850
900
950
Which number is closest to the square root of 1000?
31
32
33
34
What is the square of 25?
575
600
625
650
Which number is a perfect square close to 1000?
961
980
995
1005
What is the square root of 900?
28
29
30
31
Which number squared equals 841?
28
29
30
31
What is the approximate value of the square root of 1024?
31
32
33
34
What is the square of 20?
300
350
400
450
Which number squared gives a result closest to 900?
29
30
31
32
What is the square root of 961?
30
31
32
33
Before you leave, take our quick quiz to enhance your learning!

